Einführung in die Paneldatenanalyse
Definition von Paneldaten:
- Beobachtung derselben Individuen über mehrere Zeitpunkte
- typische Beispiele: sozio-ökonomisches Panel (SOEP), Unternehmensdaten über Jahre
- Beobachtung derselben Individuen über mehrere Zeitpunkte
Struktur eines Paneldatensatzes:
- \(y_{it}\): abhängige Variable für Individuum \(i\) zu Zeitpunkt \(t\)
- \(x_{it}\): Vektor unabhängiger Variablen für Individuum \(i\) zu Zeitpunkt \(t\)
- \(i = 1, \dots, N\), \(t = 1, \dots, T\)
- \(y_{it}\): abhängige Variable für Individuum \(i\) zu Zeitpunkt \(t\)
zur Veranschaulichung:

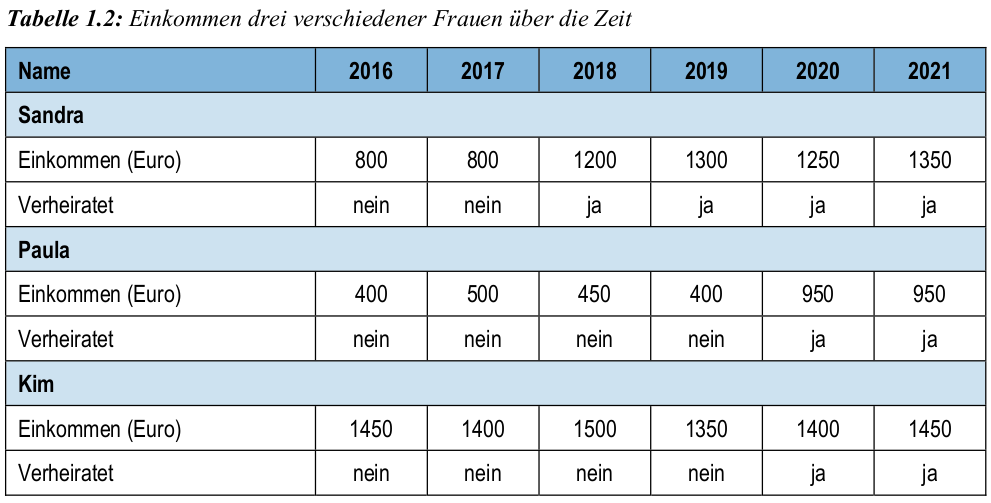
Lineares Modell für Paneldaten
Definition: klassische lineare Regression für Paneldaten:
Annahme: Effekte der unabhängigen Variablen sind konstant über Individuen und Zeit
\[ y_{it} = \beta_0 + \beta_1 x_{it}^{(1)} + \dots + \beta_D x_{it}^{(D)} + \epsilon_{it} \]
Matrixnotation: Zusammenfassung der unabhängigen Variablen als Vektor
\(X_{it} = (x_{it}^{(1)}, x_{it}^{(2)}, \dots, x_{it}^{(D)})^\top\) führt, mit \(\beta=(\beta_1,\ldots,\beta_D)\) als Vektor der Regressionskoeffizienten, zum Modell in kompakter Form:\[ y_{it} = \beta_0 + X_{it}^\top \beta + \epsilon_{it} \]
Implikationen des Modells und Problematik:
Falls alle unabhängigen Variablen \(X_{it} = 0\) sind, so ist \(\beta_0\) der Durchschnittswert von \(y_{it}\) in Abwesenheit von erklärenden Variablen und \(\epsilon_{it}\) allein erfasst unbeobachtete Einflüsse:
\[ y_{it} = \beta_0 + \epsilon_{it} \]
Annahme homogener Effekte für alle Individuen und Zeitpunkte oft nicht realistisch
alle erklärenden Variablen Null \(\ra\) Modell impliziert: alle Individuen haben denselben Grundwert \(\beta_0\)
Dies würde bedeuten, dass Unterschiede in \(y_{it}\) nur durch Zufall entstehen
Beispiel: Personen mit gleicher Bildung verdienen unterschiedlich, was das Modell nicht erklärt
Realität: unbeobachtete Faktoren (soziale Herkunft, Talent, Netzwerke) beeinflussen Einkommen
Das einfache Modell kann diese individuellen Effekte (individuelle Heterogenität) nicht erfassen
Effects-Modelle
Grundidee des Effects-Modells:
Erweiterung des linearen Modells um individuelle Grundwerte \(\alpha_i\) für jedes Individuum
Annahme: jedes Individuum besitzt einen eigenen Basiswert für die abhängige Variable
allgemeine Modellform:
\[ y_{it} = \alpha_i + X_{it}^\top \beta + \epsilon_{it}, \quad \forall i=1, \ldots,N, \quad t=1,\ldots,T \]
individuelle Effekte \(\alpha_i\) repräsentieren unbeobachtete Charakteristika (z. B. Talent/soziale Herkunft)
Interpretation der Modellparameter:
- \(\alpha_i\) beschreibt den erwarteten Grundwert von \(y_{it}\) über alle Zeitpunkte \(t\), wenn \(X_{it} = 0\)
- \(\beta_j\) misst den Einfluss der unabhängigen Variable \(x_{it}^{(j)}\) auf \(y_{it}\)
- \(\epsilon_{it}\) ist ein zufälliger Fehlerterm, der unbeobachtete Schwankungen enthält
- \(\alpha_i\) beschreibt den erwarteten Grundwert von \(y_{it}\) über alle Zeitpunkte \(t\), wenn \(X_{it} = 0\)
Mathematische Darstellung der unbeobachteten Heterogenität:
Modellierung der individuellen Effekte führt zur Modellform:
\[ y_{it} = \alpha_i + X_{it}^\top \beta + \epsilon_{it}, \quad i = 1, \dots, N, \quad t = 1, \dots, T \]
individuelle Effekte \(\alpha_i\) können als feste (fixed) oder zufällige (random) Effekte behandelt werden
Statistische Annahmen an das Effects-Modell
(A1) Strikte Exogenität:
Die Fehlerterme \(\epsilon_{it}\) sind unkorreliert mit den unabhängigen Variablen \(X_{it}\) und \(\alpha_i\):
\[ \mathbb{E}[\epsilon_{it} | X_{it}, \alpha_i] = 0 \quad \forall i=1,\ldots, N \ \text{und} \ t=1,\ldots,T \]
falls verletzt \(\ra\) Endogenität \(\ra\) verzerrte Schätzungen \(\ra\) PROBLEMATISCH
(A2) Unkorreliertheit der Fehler:
Die Fehlerterme sind sowohl zeitlich als auch über die Individuen hinweg unkorreliert
\[ \text{Cov}(\epsilon_{i_1 t_1}, \epsilon_{i_2 t_2}) = 0 \quad \forall (i_1, t_1) \neq (i_2, t_2) \]
Falls verletzt \(\ra\) Autokorrelation \(\ra\) verschlechtert Effizienz (nicht mehr BLUE)
(A3) Homoskedastizität:
Fehler haben über die Zeit und über die Individuen hinweg konstante Varianz
\[ \text{Var}(\epsilon_{it}) = \sigma^2 \quad \forall i, t \]
Falls verletzt \(\ra\) Heteroskedastizität \(\ra\) verschlechtert Effizienz (nicht mehr BLUE)
(A4) Keine Multikollinearität: Einzelne Kovariate, also Komponenten aus
\(X_{it}=(x_{it}^{(1)}, \ldots, x_{it}^{(D)})^\top\), sind nicht kollinear,- kein \(x_{it}^{(d)}\) ist Linearkombination der (einer) anderen — Informationswert einer Variablen lässt sich nicht durch die anderen ausdrücken — falls verletzt \(\ra\) hohe Standardfehler
FE-Modell (A5F): \(\alpha_i\) deterministisch
RE-Modell (A5R): \(\text{Cov}(\alpha_i,X_{it})=0\) und
\(\alpha_i \sim (\mu=\alpha,\sigma_{\alpha}^2)\)
Fixed- und Random-Effects
Grundidee der Effekte:
Beide Modelle basieren auf der Modellgleichung:
\[ y_{it} = \alpha_i + X_{it}^\top \beta + \epsilon_{it} \]
Unterschied liegt in der Interpretation der individuellen Effekte \(\alpha_i\)
Fixed-Effects-Modell (FE-Modell):
- Annahme: \(\alpha_i\) sind deterministische Individuen-spezifische Effekte, \(\alpha_i\) kann mit \(X_{it}\) korrelieren
- Individuelle Unterschiede werden explizit, als fester Mittelwert für
- B. jedes Individuum modelliert \(\ra\) geeignet, wenn \(N\) klein ist und sich Individuen systematisch unterscheiden (z. B. unterschiedliche Länder)
Random-Effects-Modell (RE-Modell):
- Annahme: \(\alpha_i\) sind zufällige Ziehungen aus einer Verteilung mit \(\alpha_i \sim \mathcal{N}(\alpha, \sigma_{\alpha}^2)\)
- Individuelle Unterschiede werden als Zufallsvariable betrachtet, gut geeignet, wenn die Individuen eine zufällige Stichprobe aus einer größeren Population darstellen \(\ra\) ACHTUNG: \(\text{Cov}(X_{it}, \alpha_i) = 0\)
- Annahme: \(\alpha_i\) sind zufällige Ziehungen aus einer Verteilung mit \(\alpha_i \sim \mathcal{N}(\alpha, \sigma_{\alpha}^2)\)
Statistische Abwägung:
- Fixed-Effects-Modell erlaubt konsistente Schätzung, auch wenn $(X_{it}, _i) $
- Random-Effects-Modell führt zu effizienteren Schätzungen, aber nur wenn $(X_{it}, _i) = 0 $
- Wahl zwischen beiden Modellen häufig mittels Hausman-Test (siehe späteres Kapitel)
- Fixed-Effects-Modell erlaubt konsistente Schätzung, auch wenn $(X_{it}, _i) $
