ar_garch – Grundlagen der Datenanalyse (GDA)

AR-Modelle

AR-Modell Einführung

Definition:
- Autoregressive Modelle beschreiben Zeitreihen, bei denen der aktuelle Wert von vergangenen Werten abhängt. Die Ordnung \(q\) bestimmt, wie viele vergangene Werte Einfluss haben.
- Beispiel: \[ x_t = \phi_1 x_{t-1} + \phi_2 x_{t-2} + \dots + \phi_q x_{t-q} + \epsilon_t \]
AR(q)-Modelle:
- AR(1): Nur vorheriger Wert beeinflusst aktuellen Wert.
- AR(2): Zwei vorherige Werte bestimmen aktuellen Wert.
- AR(q): \(q\) vorherige Werte haben Einfluss.
Voraussetzungen: Stationarität, keine stark ausgeprägten Trends oder saisonalen Komponenten.
Anwendungsbereich: Finanzmarktanalysen, Wirtschaftsindikatoren, Wetterprognosen.

ARCH-Modelle Einführung

Idee: Modellierung von Renditen als \(r_t = \mu_t + \epsilon_t\).
- Bei täglichen Renditen meist keine Autokorrelation, sodass man einfach \(\mu_t \equiv \mu\) setzt.
- Dann gilt \(r_t - \mu = \epsilon_t\) und man modelliert weiter \(\epsilon_t = \sigma_t u_t\) mit \(u_t \sim\) starker WN.
- Nun gilt \(Var[\epsilon_t] = Var[\sigma_t u_t] = \sigma_t^2 Var[u_t] = \sigma_t^2 \cdot 1 = \sigma_t^2\).
Definition:
- Autoregressive Conditional Heteroscedasticity (ARCH) modelliert die Varianz der Fehlerzeitreihe.
- Annahme: Varianz hängt von vergangenen Fehlerwerten ab.
ARCH(1)-Modell:
- Einfachste Form: Varianz \(\sigma_t^2\) hängt von vorherigem Fehlerterm \(\epsilon_{t-1}\) ab.
- Mathematisch: \[ \sigma_t^2 = \omega + \alpha_1 \epsilon_{t-1}^2 \] wobei \(\omega\) und \(\alpha_1\) zu schätzen sind.
ARCH(q)-Modell:
- Erweiterung auf mehrere vorherige Fehlerwerte: \[ \sigma_t^2 = \omega + \sum_{i=1}^{q} \alpha_i \epsilon_{t-i}^2 \]
Anwendungsbereich: Finanzmärkte, Volatilitätsmodellierung, Risikoanalysen.

Implementierung von ARCH-Modellen in `R`

Daten Einlesen (Kapitel 3.5)

# install.packages("tsibbledata"); install.packages("PerformanceAnalytics")
library(magrittr)
library(xts)

Loading required package: zoo


Attaching package: 'zoo'

The following objects are masked from 'package:base':

    as.Date, as.Date.numeric

library(PerformanceAnalytics)


Attaching package: 'PerformanceAnalytics'

The following object is masked from 'package:graphics':

    legend

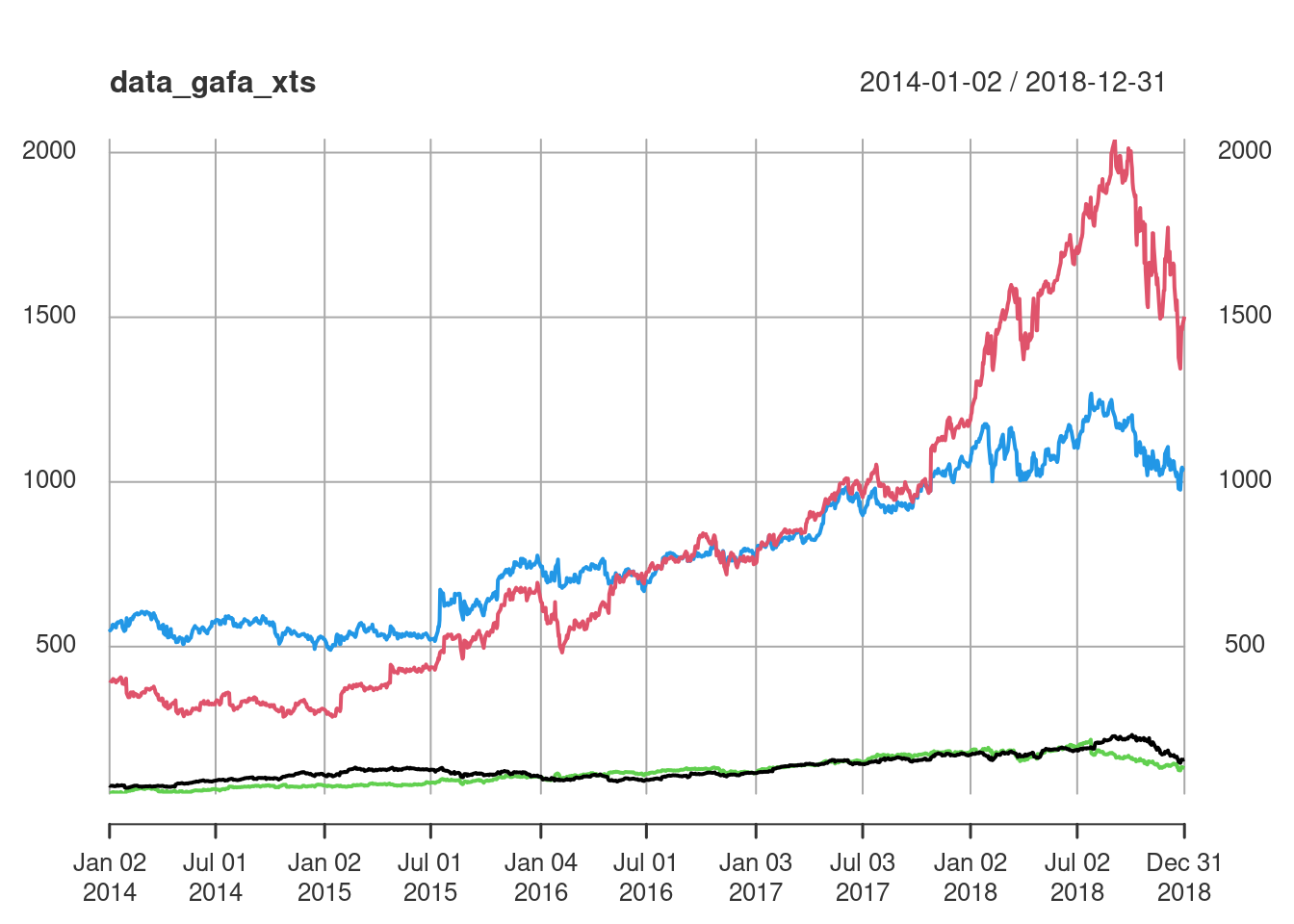
data_gafa <- tsibbledata::gafa_stock %>% 
  dplyr::select(Date, Symbol, Close) %>%
  tidyr::pivot_wider(names_from = Symbol, values_from = Close)
colnames(data_gafa) <- c("Date", "Apple","Amazon", "Facebook", "Google")
head(data_gafa)

# A tibble: 6 × 5
  Date       Apple Amazon Facebook Google
  <date>     <dbl>  <dbl>    <dbl>  <dbl>
1 2014-01-02  79.0   398.     54.7   553.
2 2014-01-03  77.3   396.     54.6   549.
3 2014-01-06  77.7   394.     57.2   555.
4 2014-01-07  77.1   398.     57.9   566.
5 2014-01-08  77.6   402.     58.2   567.
6 2014-01-09  76.6   401.     57.2   561.

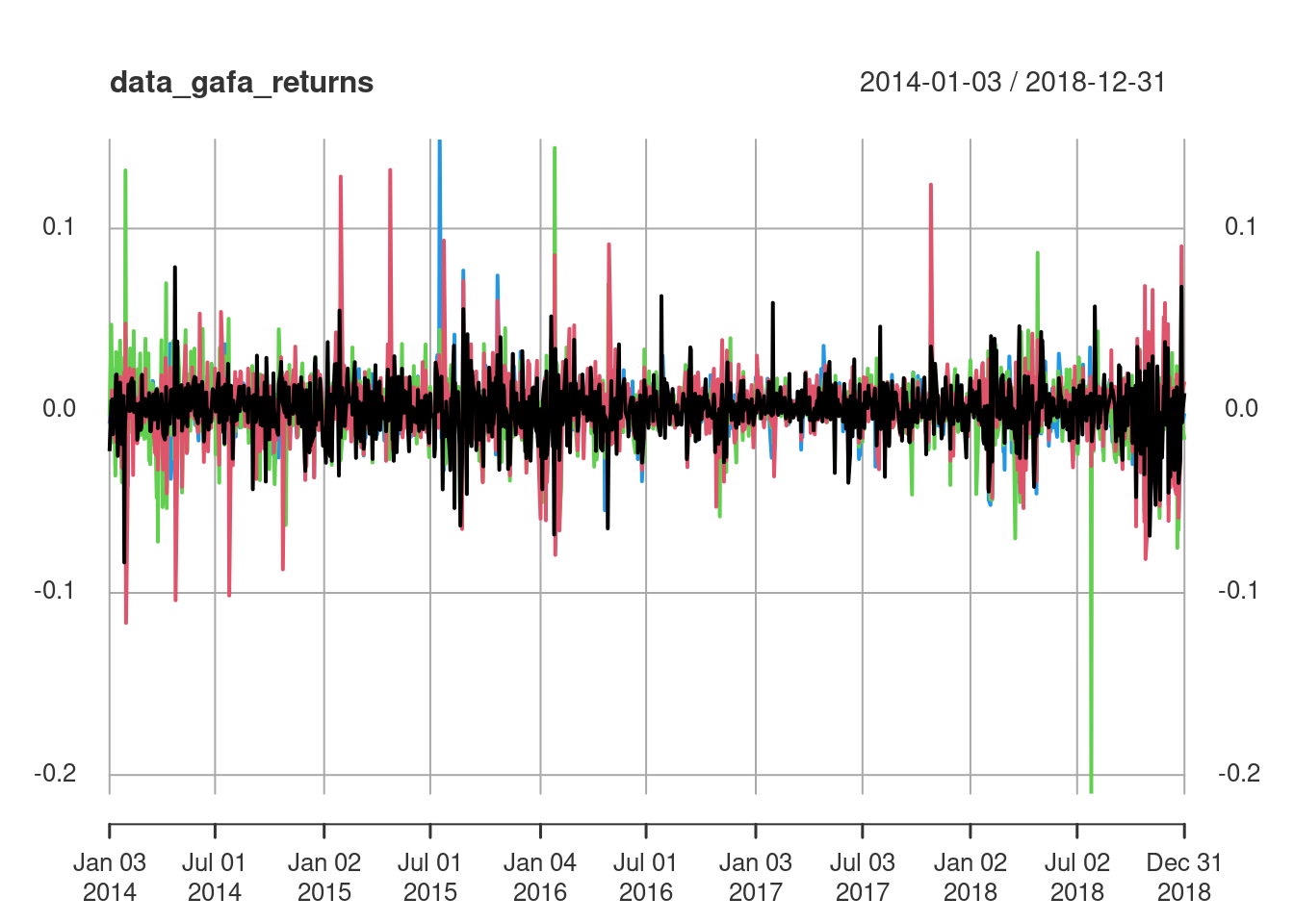
data_gafa_xts <- xts::xts(data_gafa[, 2:5], order.by = data_gafa$Date)
data_gafa_returns <- PerformanceAnalytics::Return.calculate(data_gafa_xts, method = "log")[-1]

Plotten der eingelesenen Daten I

library(xts)
plot(data_gafa_xts)

Plotten der eingelesenen Daten II

library(xts)
plot(data_gafa_returns)

Überprüfung von Annahmen

Gibt es ARCH-Effekte?

Standardabweichung als Maß für Volatilität.
Hohe Standardabweichung \(\ra\) große Schwankungen.
Niedrige Standardabweichung \(\ra\) stabile Zeitreihe.
Gleitende Standardabweichung: jährliche Normierung.
Berechnung für Apple-Daten über 22-Tage-Fenster: viele Werte \(> 0.2\) deuten auf hohe Volatilität hin.

PerformanceAnalytics::chart.RollingPerformance(
  R = data_gafa_returns$Apple, width = 22, FUN = 'sd.annualized')

Visuell scheint es welche zu geben, daher nun formale Tests.
Vorher: Renditedaten stationarisieren (z. B. HP-Filter).

# install.packages("FinTS"); install.packages("mFilter")
return_data_apple_filtered <- mFilter::mFilter(ts(data_gafa_returns$Apple), filter = "HP")
return_data_apple_filtered <- xts::as.xts(return_data_apple_filtered$x)
FinTS::ArchTest(return_data_apple_filtered)


    ARCH LM-test; Null hypothesis: no ARCH effects

data:  return_data_apple_filtered
Chi-squared = 39.912, df = 12, p-value = 7.436e-05

\(H_0\): Keine ARCH-Effekte.
Ergebnis: \(H_0\) abgelehnt, ARCH-Effekte vorhanden.

Schätzung von ARCH-Modellen

# install.packages("rugarch")
model_specification_apple_arch <- rugarch::ugarchspec(
  variance.model =
    list(
      model = 'sGARCH',
      garchOrder = c(1, 0) # Erstes Element: ARCH-Ordnung, zweites = 0 für ARCH
    ), 
  mean.model = list(
    armaOrder = c(0, 0)
  ),
  distribution.model = "norm")
fit_ARCH_data_apple <- rugarch::ugarchfit(
  data = return_data_apple_filtered,
  spec = model_specification_apple_arch
)

Alle Parameter signifikant (p < 0.05).
Modell: \[ \sigma_t^2 = 3\times 10^{-6} + 0.999\cdot e_{t-1}^2 \]

Ergebnisse ausgeben

print(fit_ARCH_data_apple)


*---------------------------------*
*          GARCH Model Fit        *
*---------------------------------*

Conditional Variance Dynamics   
-----------------------------------
GARCH Model : sGARCH(1,0)
Mean Model  : ARFIMA(0,0,0)
Distribution    : norm 

Optimal Parameters
------------------------------------
        Estimate  Std. Error   t value Pr(>|t|)
mu      0.052183    0.000012 4459.5219        0
omega   0.000003    0.000000    7.6727        0
alpha1  0.999000    0.000146 6829.2296        0

Robust Standard Errors:
        Estimate  Std. Error  t value Pr(>|t|)
mu      0.052183    3.995753 0.013060  0.98958
omega   0.000003    0.077704 0.000043  0.99997
alpha1  0.999000   76.882235 0.012994  0.98963

LogLikelihood : 1412.957 

Information Criteria
------------------------------------
                    
Akaike       -2.2434
Bayes        -2.2311
Shibata      -2.2434
Hannan-Quinn -2.2388

Weighted Ljung-Box Test on Standardized Residuals
------------------------------------
                        statistic   p-value
Lag[1]                      14.12 0.0001716
Lag[2*(p+q)+(p+q)-1][2]     14.21 0.0001485
Lag[4*(p+q)+(p+q)-1][5]     15.89 0.0002562
d.o.f=0
H0 : No serial correlation

Weighted Ljung-Box Test on Standardized Squared Residuals
------------------------------------
                        statistic p-value
Lag[1]                    0.01666  0.8973
Lag[2*(p+q)+(p+q)-1][2]   0.01848  0.9820
Lag[4*(p+q)+(p+q)-1][5]   0.04717  0.9996
d.o.f=1

Weighted ARCH LM Tests
------------------------------------
            Statistic Shape Scale P-Value
ARCH Lag[2]  0.003628 0.500 2.000  0.9520
ARCH Lag[4]  0.013470 1.397 1.611  0.9990
ARCH Lag[6]  0.067159 2.222 1.500  0.9996

Nyblom stability test
------------------------------------
Joint Statistic:  2.5469
Individual Statistics:             
mu     0.5887
omega  0.1785
alpha1 0.5888

Asymptotic Critical Values (10% 5% 1%)
Joint Statistic:         0.846 1.01 1.35
Individual Statistic:    0.35 0.47 0.75

Sign Bias Test
------------------------------------
                   t-value      prob sig
Sign Bias           0.6081 5.432e-01    
Negative Sign Bias  5.1984 2.346e-07 ***
Positive Sign Bias  0.7707 4.411e-01    
Joint Effect       29.6145 1.663e-06 ***


Adjusted Pearson Goodness-of-Fit Test:
------------------------------------
  group statistic p-value(g-1)
1    20      2836            0
2    30      2853            0
3    40      2864            0
4    50      2860            0


Elapsed time : 0.8626037

Visualisierung der Ergebnisse

library("rugarch")
plot(fit_ARCH_data_apple, which = "all")


please wait...calculating quantiles...

Vorhersagen mit ARCH-Modell

forcast_ARCH_apple <- rugarch::ugarchforecast(fitORspec = fit_ARCH_data_apple, n.ahead = 5)
forcast_ARCH_apple


*------------------------------------*
*       GARCH Model Forecast         *
*------------------------------------*
Model: sGARCH
Horizon: 5
Roll Steps: 0
Out of Sample: 0

0-roll forecast [T0=1257-01-01]:
     Series   Sigma
T+1 0.05218 0.04258
T+2 0.05218 0.04260
T+3 0.05218 0.04262
T+4 0.05218 0.04264
T+5 0.05218 0.04265

GARCH-Modelle

Einführung

Idee wie bei ARCH:
- Modellierung von Renditen als \(r_t = \mu_t + \epsilon_t\).
- \(r_t - \mu = \epsilon_t\), \(\epsilon_t = \sigma_t u_t\), \(u_t \sim\) starker WN.
- \(Var[\epsilon_t] = \sigma_t^2\).
Definition:
- Generalized Autoregressive Conditional Heteroscedasticity.
- Annahme: Varianz hängt von vergangenen Fehlern UND vorherigen Varianzen ab.
GARCH(q, p)-Modell:
- \(\sigma_t^2 = \omega + \sum_{i=1}^q \alpha_i \epsilon_{t-i}^2 + \sum_{j=1}^p \beta_j \sigma_{t-j}^2\)
- q bestimmt die Anzahl der berücksichtigten Verzögerungen der Fehlerterme
- p bestimmt die Anzahl der berücksichtigten Verzögerungen der Varianzen
Anwendungsbereich: wie bei ARCH.

GARCH in `R`

library("rugarch")
model_specification_apple_garch <- ugarchspec(
  variance.model = 
    list(model = "sGARCH",
         garchOrder = c(1, 1)),
  mean.model = 
    list(armaOrder = c(0, 0)),
  distribution.model = "norm")
fit_GARCH_data_apple <- ugarchfit(
  data = return_data_apple_filtered,
  spec = model_specification_apple_garch)

wieder: alle Parameter sind signifikant mit Niveau 5% (p < 0.05).
das geschätzte / angepasste GARCH-Modell lautet: \[ \sigma_t^2 = 0.000025 + 0.122304\cdot e_{t-1}^2 + 0.771785\cdot \sigma_{t-1}^2 \]

Ergebnisse ausgeben

print(fit_GARCH_data_apple)


*---------------------------------*
*          GARCH Model Fit        *
*---------------------------------*

Conditional Variance Dynamics   
-----------------------------------
GARCH Model : sGARCH(1,1)
Mean Model  : ARFIMA(0,0,0)
Distribution    : norm 

Optimal Parameters
------------------------------------
        Estimate  Std. Error  t value Pr(>|t|)
mu      0.001146    0.000388   2.9519 0.003158
omega   0.000025    0.000006   3.9852 0.000067
alpha1  0.122303    0.028784   4.2491 0.000021
beta1   0.771789    0.046595  16.5637 0.000000

Robust Standard Errors:
        Estimate  Std. Error  t value Pr(>|t|)
mu      0.001146    0.000421   2.7222 0.006484
omega   0.000025    0.000010   2.6473 0.008114
alpha1  0.122303    0.033481   3.6529 0.000259
beta1   0.771789    0.058764  13.1338 0.000000

LogLikelihood : 3538.843 

Information Criteria
------------------------------------
                    
Akaike       -5.6243
Bayes        -5.6079
Shibata      -5.6243
Hannan-Quinn -5.6181

Weighted Ljung-Box Test on Standardized Residuals
------------------------------------
                        statistic p-value
Lag[1]                      1.496  0.2213
Lag[2*(p+q)+(p+q)-1][2]     1.640  0.3301
Lag[4*(p+q)+(p+q)-1][5]     2.435  0.5197
d.o.f=0
H0 : No serial correlation

Weighted Ljung-Box Test on Standardized Squared Residuals
------------------------------------
                        statistic p-value
Lag[1]                    0.09701  0.7554
Lag[2*(p+q)+(p+q)-1][5]   0.68386  0.9260
Lag[4*(p+q)+(p+q)-1][9]   1.07587  0.9829
d.o.f=2

Weighted ARCH LM Tests
------------------------------------
            Statistic Shape Scale P-Value
ARCH Lag[3]   0.06627 0.500 2.000  0.7969
ARCH Lag[5]   0.82619 1.440 1.667  0.7851
ARCH Lag[7]   0.96451 2.315 1.543  0.9193

Nyblom stability test
------------------------------------
Joint Statistic:  0.4744
Individual Statistics:              
mu     0.04709
omega  0.09750
alpha1 0.14804
beta1  0.11503

Asymptotic Critical Values (10% 5% 1%)
Joint Statistic:         1.07 1.24 1.6
Individual Statistic:    0.35 0.47 0.75

Sign Bias Test
------------------------------------
                   t-value   prob sig
Sign Bias           0.3940 0.6936    
Negative Sign Bias  0.5946 0.5522    
Positive Sign Bias  0.5933 0.5531    
Joint Effect        2.6375 0.4510    


Adjusted Pearson Goodness-of-Fit Test:
------------------------------------
  group statistic p-value(g-1)
1    20     84.91    2.612e-10
2    30    103.60    2.579e-10
3    40    109.40    1.343e-08
4    50    118.62    1.053e-07


Elapsed time : 0.1914036

Vorhersagen mit GARCH-Modell

forcast_GARCH_apple <- rugarch::ugarchforecast(fitORspec = fit_GARCH_data_apple, n.ahead = 5)
forcast_GARCH_apple


*------------------------------------*
*       GARCH Model Forecast         *
*------------------------------------*
Model: sGARCH
Horizon: 5
Roll Steps: 0
Out of Sample: 0

0-roll forecast [T0=1257-01-01]:
      Series   Sigma
T+1 0.001146 0.02301
T+2 0.001146 0.02233
T+3 0.001146 0.02171
T+4 0.001146 0.02114
T+5 0.001146 0.02061

Visualisierung der Ergebnisse

library("rugarch")
plot(fit_GARCH_data_apple, which = "all")


please wait...calculating quantiles...

AR-Modelle

AR-Modell Einführung

ARCH-Modelle Einführung

Implementierung von ARCH-Modellen in R

Daten Einlesen (Kapitel 3.5)

Plotten der eingelesenen Daten I

Plotten der eingelesenen Daten II

Überprüfung von Annahmen

Gibt es ARCH-Effekte?

Schätzung von ARCH-Modellen

Ergebnisse ausgeben

Visualisierung der Ergebnisse

Vorhersagen mit ARCH-Modell

GARCH-Modelle

Einführung

GARCH in R

Ergebnisse ausgeben

Vorhersagen mit GARCH-Modell

Visualisierung der Ergebnisse

Implementierung von ARCH-Modellen in `R`

GARCH in `R`