Zeitreihen – Einleitung – Komponentenmodelle

Einführung

• Multiple lineare Regression:

  \[ AV = \beta_0 + \beta_1 UV_1 + \dots + \beta_n UV_n \]

  Standardregression, bei der die abhängige Variable (AV) durch mehrere unabhängige Variablen (UV) erklärt wird.

• Zeitabhängige Regression:

  \[ AV(t) = \beta_0 + \beta_1 UV_1(t) + \dots + \beta_n UV_n(t) \]

  Erweiterung um den Zeitfaktor ( t ), sodass alle Variablen zeitabhängig sind.

• Allgemeine Darstellung einer Zeitreihe:

  \[ \{x_t\}, \quad t \in \mathbb{N} \]

  Eine Zeitreihe ist eine Menge gerichteter Beobachtungen über die Zeit.

• Lineares Modell für eine Zeitreihe:

  \[ x_t = \beta \cdot t \]

  Einfache lineare Darstellung einer Zeitreihe, die nur einen linearen Trend abbildet.

Einführung

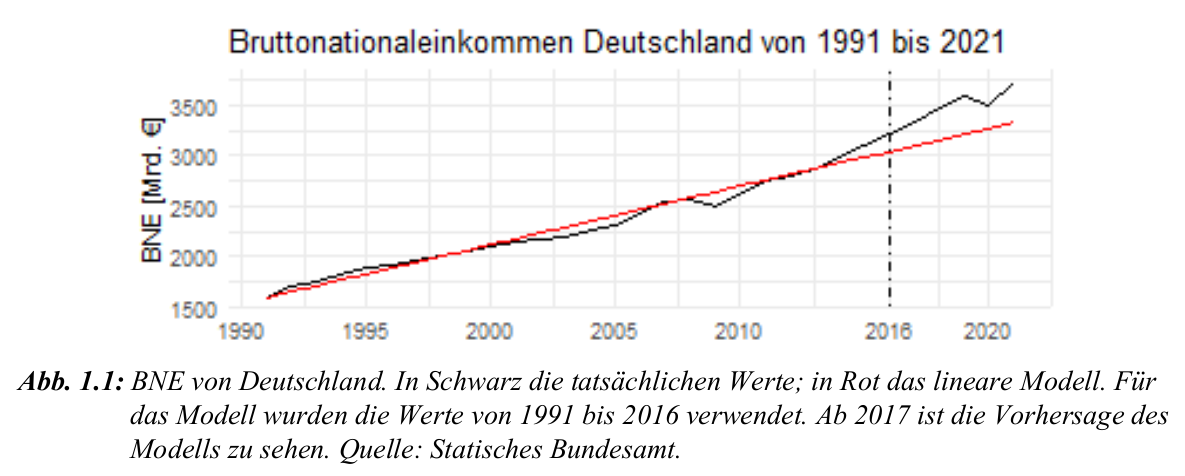
• Lineares Modell basiert auf Daten von 1991 bis 2016.
• Vorhersage für 2017–2021 zeigt deutliche Abweichungen von den tatsächlichen Werten.
• Lineares Modell erklärt Schwankungen nicht hinreichend: Vorhersage weicht von tatsächlichen Werten ab.
• Additives und multiplikatives Komponentenmodell sollen bessere Ergebnisse liefern.

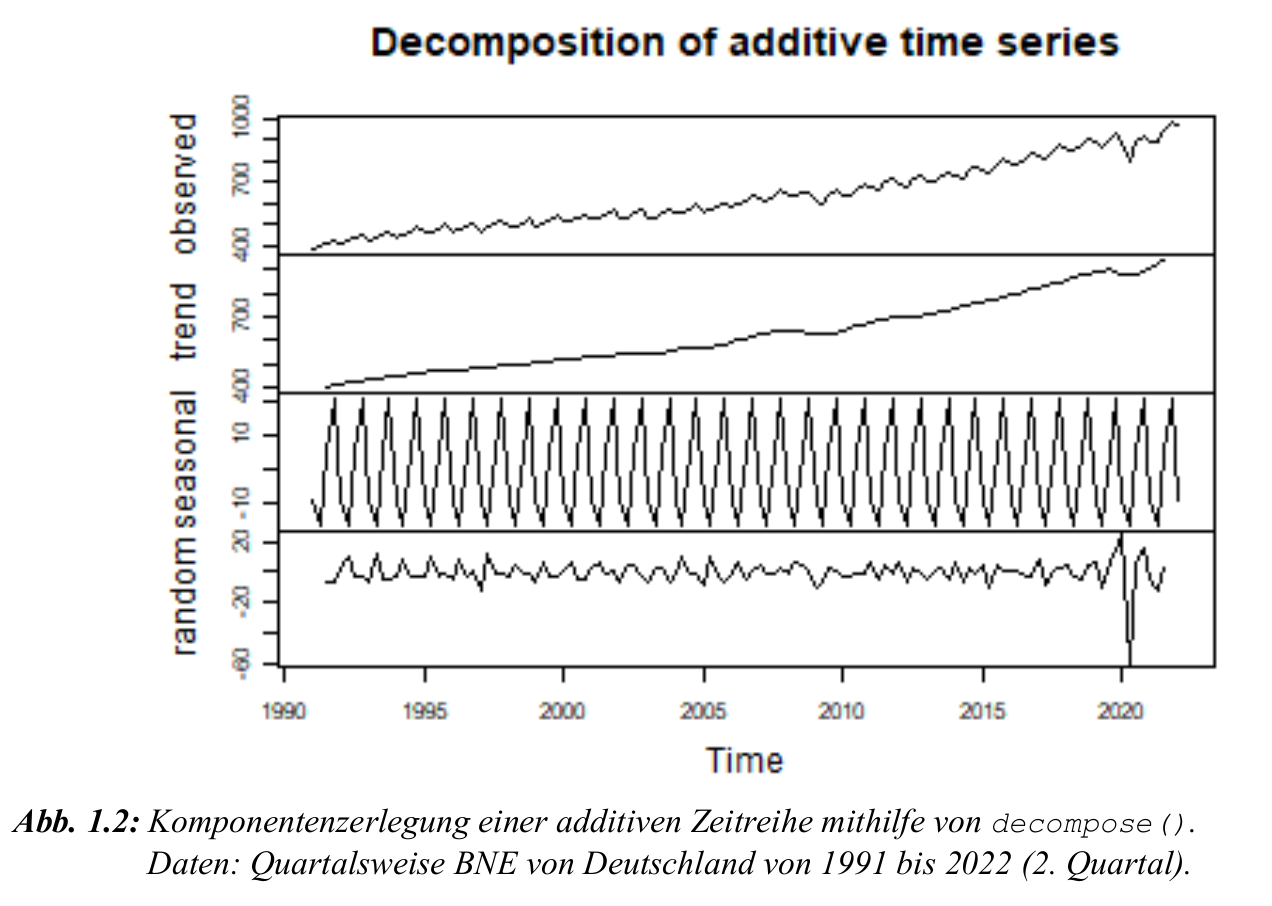
Additives Komponentenmodell

• Additives Komponentenmodell:

  • Eine Zeitreihe \(x_t\) wird in drei additive Komponenten zerlegt:

    \[ x_t = x_T(t) + x_S(t) + x_R(t) \]

  • Trendkomponente ( x_T(t) ): langfristige systematische Veränderung

  • Saisonkomponente ( x_S(t) ): regelmäßige jahreszeitliche Schwankungen

  • Restkomponente ( x_R(t) ): unregelmäßige Schwankungen — nicht durch Trend oder Saison erklärt

• Analyse in R möglich mit decompose()-Funktion.
• Beispielgrafik zeigt starke Restkomponente ab 2020 (Corona-Effekt).

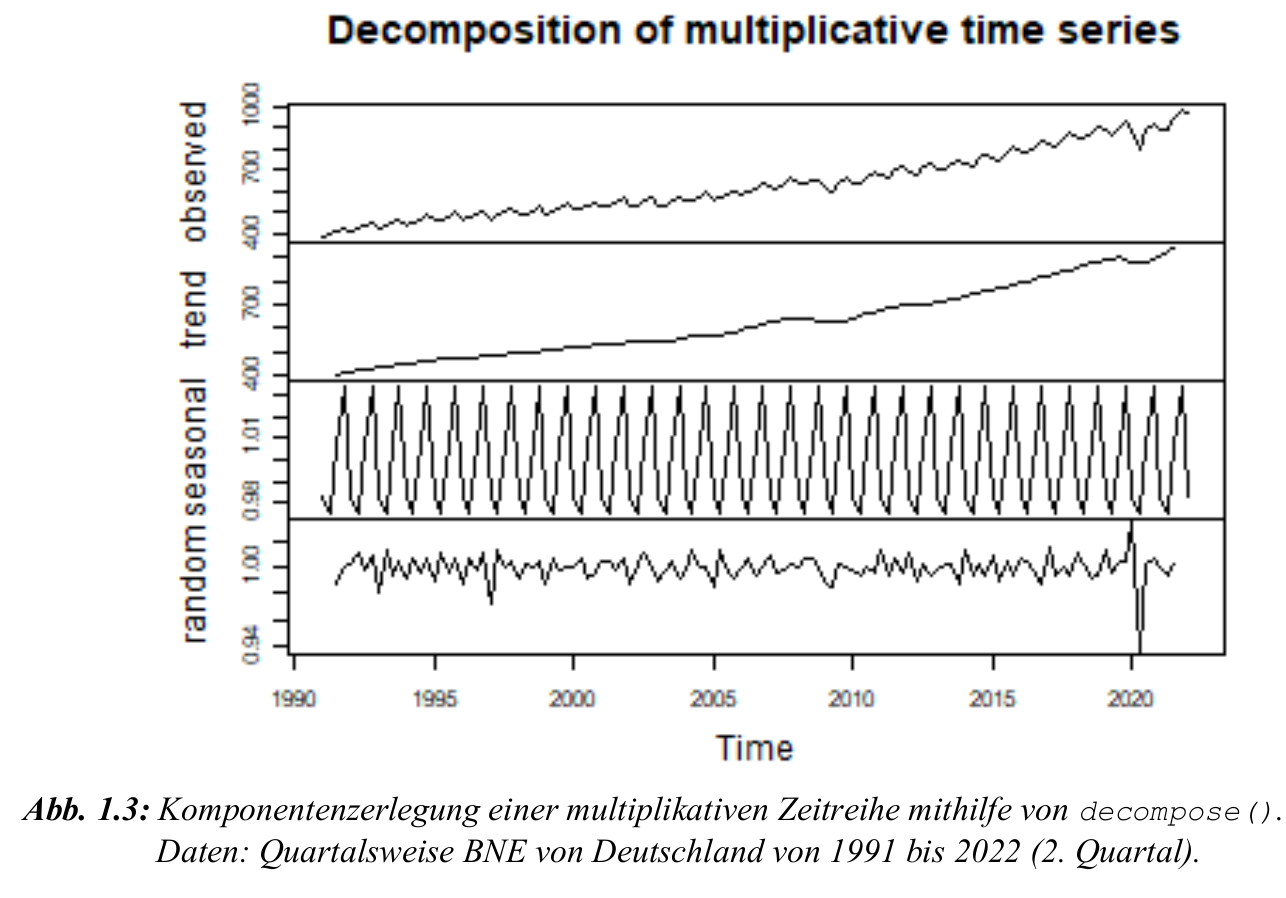
Multiplikatives Komponentenmodell

• Multiplikatives Komponentenmodell:

  • Eine Zeitreihe \(x_t\) wird in drei Komponenten zerlegt:

    \[ x_t = x_T(t) \cdot x_S(t) \cdot x_R(t) \]

  • Trendkomponente ( x_T(t) ): langfristige systematische Veränderung

  • Saisonkomponente ( x_S(t) ): jahreszeitliche Schwankungen, die mit der Zeit größer werden

  • Restkomponente ( x_R(t) ): unregelmäßige Schwankungen, die nicht durch Trend oder Saison erklärbar sind

• Wird genutzt, wenn die Streuung der Zeitreihe über die Zeit zunimmt.
• Unterschied zum additiven Modell:
  • Rest- und Saisonkomponente haben geringere Werte.
  • Modell reagiert stärker auf äußere Einflüsse (z. B. Wirtschaftskrisen).
• Beispiel: BNE-Daten zeigen stärkeren Einfluss der Asienkrise 1997 im multiplikativen Modell.

Multiplikativ zu additiv

• additiv vs. multiplikativ:

  • Additive Modelle geeignet bei konstanter saisonaler Schwankung.
  • Multiplikative Modelle, wenn Streuung der Zeitreihe mit der Zeit wächst.
  • Beispiel: Für quartalsweises BNE von Deutschland wäre ein additives Modell passend.

• Multiplikativ zu additiv transformieren:

  • Notwendig, da viele Analysen auf additiven Modellen basieren.
  • Transformation der Zeitreihe durch Logarithmieren oder Box-Cox.

• Logarithmische Transformation:

  \[ y_t = \ln(x_t) \]

• Box-Cox-Transformation:

  \[ y_t = \begin{cases} \frac{x_t^\lambda - 1}{\lambda}, & \lambda \neq 0 \\ \ln(x_t), & \lambda = 0 \end{cases} \]

  • Reduziert Heteroskedastizität (ungleiche Varianzen über die Zeit).
  • Ermöglicht Anwendung additiver Analysen auf ursprünglich multiplikative Zeitreihen.