Formale Beschreibung der Assoziationsanalyse
Grundlagen:
Ausgangspunkt: Menge von Transaktionen
\(D=\{T_1,T_2,\dots,T_n\}\) und Itemmenge \(I\), wobei jede Transaktion \(T_j \subset I\). Eine Assoziationsregel mit \(X,Y \subset I\), \(X \cap Y = \emptyset\), erfüllt eine Regel \(X \rightarrow Y\) genau dann, wenn \(X \cup Y \subset T\), und hat die Form:\[ X \rightarrow Y \]
Support:
Der Support einer Itemmenge \(X\) gibt an, wie häufig \(X\) in der Datenbank \(D\) vorkommt:\[ \text{Support}(X)= \frac{\left|\{\,T_j \in D: X \subset T_j\,\}\right|}{|D|} \]
Support einer Regel: Beschreibt, ob eine Regel relevant ist:
\[ \text{Support}(X \rightarrow Y)= \text{Support}(X \cup Y)= \frac{\left|\{\,T_j \in D: X \cup Y \subset T_j\,\}\right|}{|D|} \]
Konfidenz: Gibt an, mit welcher Wahrscheinlichkeit die Regel zutrifft.
FEHLER im SB 04, S.10: im Nenner nicht \(X \in T\), sondern \(\boldsymbol{X \subset T}\)\[ \text{Konfidenz}(X \rightarrow Y)= \frac{\text{Support}(X \cup Y)}{\text{Support}(X)}= \frac{\left|\,\{T \in D : (X \cup Y) \subset T\}\,\right|} {\left|\,\{T \in D : \boldsymbol{X \subset T}\}\,\right|} \]
Lift: Misst die Stärke der Assoziation relativ zur erwarteten Unabhängigkeit:
\[ \text{Lift}(X \rightarrow Y)= \frac{\text{Support}(X \cup Y)} {\text{Support}(X)\cdot\text{Support}(Y)} \]
- \(\text{Lift} > 1\): positive Assoziation
- \(\text{Lift} = 1\): keine Assoziation
- \(\text{Lift} < 1\): negative Assoziation
- \(\text{Lift} > 1\): positive Assoziation
Man kann zeigen: Gesamtzahl möglicher Regeln \(R\) in einem Datensatz mit \(d\) Items:
\[ R = 3^d - 2^{d+1} + 1 \]
Schritte der Assoziationsanalyse — Apriori-Algorithmus
Übersicht

Beispiel (Support 50 %, Konfidenz 60 %)
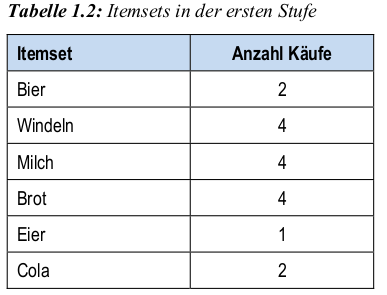
- Schritt 1 (K=1): Suche Itemsets aus 1 Produkt (\(\Leftrightarrow\) wie oft ein Produkt gekauft wird).
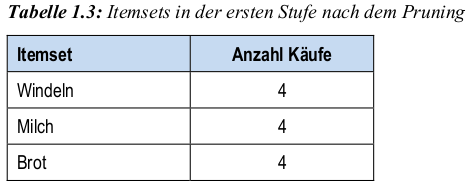
- Schritt 2 (K=1): Entferne Itemsets, die minimalen Support nicht erreichen (prune-Schritt).
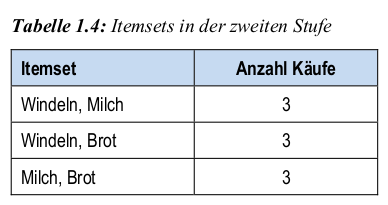
- Schritt 3 (K=2): join-Schritt wie bei Schritt 1, nur mit 2 Produkten (aus den verbliebenen Produkten).
- Schritt 4 (K=2): prune-Schritt wie Schritt 2 \(\ra\) entferne Itemsets ohne minimalen Support.

Schritt 5 (K=3)
- Bilde Itemsets, die aus 3 zusammen gekauften Produkten bestehen.


Zusätzliche Hinweise
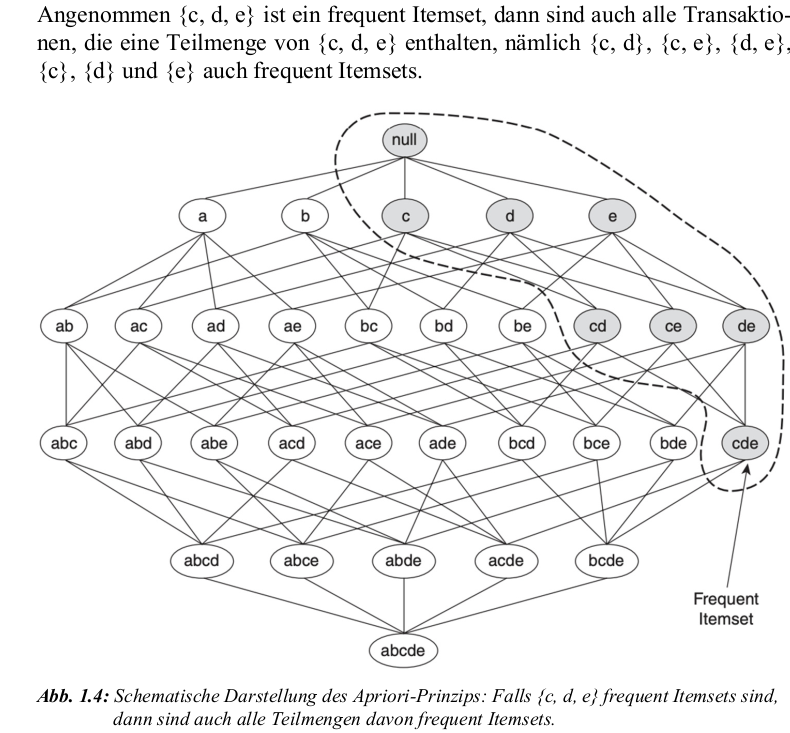
Agrawal & Srikant (1994): Wenn ein Itemset frequent ist, sind auch alle seine Teilmengen frequent Itemsets.
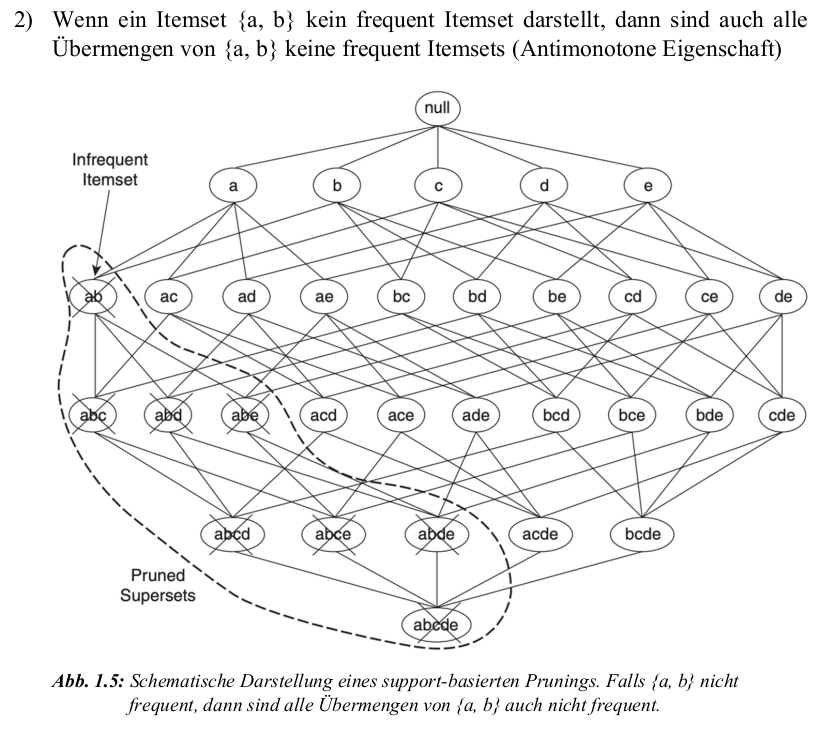
Implementierung in R
Hier nicht weiter betrachtet -> siehe Studienbrief 04, Kapitel 1.6 ff.
