Binär logistische Regression

Idee und Einführung

Idee:
- Abhängigkeit einer dichotomen Variablen von unabhängigen Variablen / Regressoren
- binär/dichotom: ja/nein, trifft zu/ trifft nicht zu, männlich/weiblich, Raucher/nicht Raucher
Dummy-Variable:
- Ebenfalls 0/1 codiert mit Bedeutung z.B. ja/nein
- wird allgemein verwendet für unabhängige und abhängige Variablen
Beispiel: Studie zur Verkehrsmittelwahl
- Pendlerfahrten: Arbeitsplatz $\ra$ zu Hause
- $\ra$ Privatauto vs. öffentlicher Nahverkehr (ÖV)
- Datensatz verkersmittel.csv mit den Variablen
- mode: Verkehrsmittel ($0 = $ Privatauto vs. $ 1 = $ ÖV)
- zeit: Fahrzeitdifferenz zwischen ÖV und Auto
- kosten: Kostendifferenz zwischen ÖV und Auto
- geschlecht: 1 = weiblich $\ra$ 2 = männlich
- umsteigen: Zahl notwendiger Umstiege bei Nutzung der ÖV
Fragestellung: Von welchen Faktoren hängt die Wahl des Verkehrsmittels ab?

Binär logistische Regression - Herleitungen

Modellgleichungen:

\[ \begin{align*} P(Y_i = 1)&=\frac{e^{\beta x_i}}{1+e^{\beta x_i}}\text{~~mit~~} \beta x_i = \beta_0 + \beta_1 x_{i1} + \ldots + \beta_k x_{ik} \\ 1 - P(Y_i = 1)&=1 - \frac{e^{\beta x_i}}{1+e^{\beta x_i}}= \frac{1+e^{\beta x_i}}{1+e^{\beta x_i}} - \frac{e^{\beta x_i}}{1+e^{\beta x_i}} = \frac{1}{1+e^{\beta x_i}} \end{align*} \]

$P(Y_i=1)$ ist die Wahrscheinlichkeit, dass abh. Variable $Y_i$ den Wert 1 annimmt, bezogen auf die Beobachtung $i$ der $i=1,\ldots,n$ Beobachtungen im Datensatz
$k$: Anzahl der unabhängigen Variablen
$x_{ik}$ der $i-$te Wert der $k$-ten unabhängigen Variablen

Odds (Oddsratio) und logarithmierte Odds (log-odds / logits):

\[ \begin{align*} Odds_{1/0}&=\frac{P(Y_i = 1)}{P(Y_i = 0)}=\frac{P(Y_i = 1)}{1-P(Y_i = 1)} =\frac{e^{\beta x_i}}{1+e^{\beta x_i}} \times 1+e^{\beta x_i}=e^{\beta x_i}\\ LogOdds_{1/0}&=\log\left(Odds_{1/0}\right)=\beta x_i = \beta_0 + \beta_1 x_{i1} + \ldots + \beta_k x_{ik} \end{align*} \]

Warning

Etwas andere Notation als im Studienbrief, aber derselbe Grundgedanke.

Binär logistische Regression - Umsetzung in `R`

Zuerst laden wir die Daten und schätzen zwei Modelle: Ein Nullmodell, das nur den Achsenabschnitt enthält, und ein Vollmodell, das alle relevanten unabhängigen Variablen berücksichtigt.

Nullmodell/Trainingsmodell vs. Testmodell

data_vkm <- read.csv("../data/verkehrsmittel.csv")
# Nullmodell: 'mode' regressiert auf Konstante '1'
model_0 <- glm(mode ~ 1,              # glm: generalisiertes lineares Modell
                   data = data_vkm,
                   family = binomial())   # logistische Regresion = Binomialmodell
  model_1 <- glm(mode ~ zeit + kosten + umsteigen + geschlecht,
                 data = data_vkm,
                 family = binomial())

glm(): generalisiertes lineares Modell (vorher: lm $\ra$ lineares Modell)
Nullmodell: ein Modell mit nur Achsenabschnitt ist gleich einer Mittelwertsregression: $\bar{Y}=\frac{1}{n}\sum_{i=1}^n Y_i$ $=\frac{1}{n} (n_{1} \times 1 + n_{0}\times 0)=\frac{n_1}{n}$; Anteil Einsen an gesamten Beobachtungen; sind im Datensatz 25-Einsen und 75-Nullen dann ergibt die Nullmodell-Regression $0.25= 25\%$ der $n=100$ Personen nutzen ÖV.

Die Zusammenfassung des Nullmodells zeigt diesen Mittelwert.

summary(model_0)


Call:
glm(formula = mode ~ 1, family = binomial(), data = data_vkm)

Coefficients:
            Estimate Std. Error z value Pr(>|z|)
(Intercept)  -0.1515     0.1839  -0.824     0.41

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 164.29  on 118  degrees of freedom
Residual deviance: 164.29  on 118  degrees of freedom
AIC: 166.29

Number of Fisher Scoring iterations: 3

Anschließend betrachten wir das volle Modell.

summary(model_1)


Call:
glm(formula = mode ~ zeit + kosten + umsteigen + geschlecht, 
    family = binomial(), data = data_vkm)

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) -3.38784    1.00131  -3.383 0.000716 ***
zeit         0.09703    0.04743   2.046 0.040793 *  
kosten      -0.01127    0.02501  -0.451 0.652134    
umsteigen    0.22231    0.55866   0.398 0.690680    
geschlecht   1.04516    0.46406   2.252 0.024308 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 164.29  on 118  degrees of freedom
Residual deviance: 120.55  on 114  degrees of freedom
AIC: 130.55

Number of Fisher Scoring iterations: 5

Interpretation

Signifikanz: Zeitdifferenz ($p = 0.04$) & Geschlecht ($p = 0.02$) sind signifikant. Umsteigezeit & Kosten sind insignifikant.
Vorzeichen: Ein positives Vorzeichen deutet auf einen positiven Effekt hin, ein negatives auf einen negativen Effekt.
Dummy-Variable Geschlecht: Die kleinere Codierung (Frau=1) ist die Referenzkategorie zu Mann=2. Der positive Koeffizient $\beta_{4}=1.04516 > 0$ zeigt einen positiven Effekt für Männer. Intern codiert R dies als 0/1, sodass der Wechsel von $x_{4}=$Frau$=0$ zu $x_{4}=$Mann$=1$ den Logit um $\beta_4 = 1.04516$ erhöht.
Die Wahrscheinlichkeit $P(Y_i =1)$, dass eine Person $i$ das Privatauto nutzt, erhöht sich bei Männern.
AIC-Vergleich: $AIC_0 = 166.29 > AIC_1 = 130.55$: Je kleiner der AIC, desto besser der Modellfit. Der absolute Wert ist nicht interpretierbar, nur der Vergleich zwischen Modellen ist aussagekräftig.

Nullmodellabweichung: Omnibus-Test

Idee:
- Vergleich zwischen Nullmodell (nur Achsenabschnitt) und Testmodell mit erklärenden Variablen.
- Testet, ob das Modell insgesamt einen signifikanten Erklärungsbeitrag leistet.
- Basis: Differenz der Abweichungen (Deviance) zwischen den Modellen.
Teststatistik:
- Chi-Quadrat-Wert: ( ^2 = - )
- Freiheitsgrade: ( df = {} - {} )
- Signifikanzbewertung: ( p = 1 - (^2, df) )

R-Umsetzung:

# Berechnung der Omnibus-Teststatistik
model_chi2 <- model_1$null.deviance - model_1$deviance
chi2_df    <- model_1$df.null - model_1$df.residual
chi2_p     <- 1 - pchisq(model_chi2, chi2_df)
print(cbind(model_chi2, chi2_df, chi2_p))

     model_chi2 chi2_df       chi2_p
[1,]   43.73964       4 7.266406e-09

Interpretation:
- Wenn ( p < 0.05 ): Modell signifikant besser als das Nullmodell.
- Wenn ( p ): Modell verbessert sich nicht signifikant.
- Beispielergebnisse: ( ^2 = 43.74, df = 4, p = 7.26 ^{-9} )

Modellgüte: Odds Ratio

Problem und Motivation:
- Problem: bisherige Schätzparameter nicht aussagekräftig, bis auf VZ
- Grund: keine lineare Funktion (wo der Effekt direkt ablesbar ist), sondern $logits$
- Ziel: wie stark beeinflusst unabh. Variable Ergebnis – Chancenverhältnis zwischen den Modellen
Odds Ratio (OR): Begriffe und Interpretation
- Odds: Chance – Oddsratio: Chancenverhältnis, im Beispiel unten Chance für Verkehrsmittelwahl ÖV vs. Auto bei Frauen im vgl. zu Männern – Logit: logarithmierte Odds
- ( OR > 1 ) steigert Wahrscheinlichkeit, ( OR < 1 ) senkt sie, ( OR = 1 ) bedeutet keine Veränderung
Odds Ratio – Beispiel: \[ OR=\frac{M\text{Ö} / MA}{F\text{Ö} / FA} = \frac{M\text{Ö} \cdot FA}{MA \cdot F\text{Ö}} \] wobei hier der erste Buchstabe Mann/Frau bezeichnet ($M$ oder $F$) und der zweite das gewählte Verkehrsmittel $Ö$ für ÖV und $A$ für Auto, z.B. FÖ für Frauen und öffentliche Verkehrsmittel.

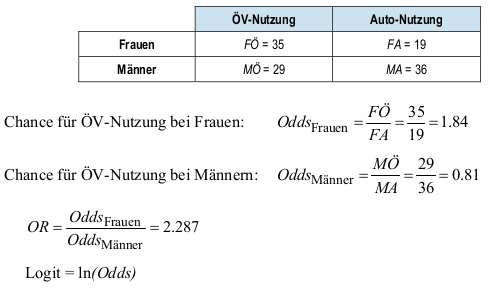
Umsetzung in `R`:

# Berechnung der Odds Ratios
exp(cbind(OR = coef(model_1)))

                   OR
(Intercept) 0.0337816
zeit        1.1018961
kosten      0.9887895
umsteigen   1.2489557
geschlecht  2.8438543

model_wm_only <- glm(mode ~ geschlecht, data = data_vkm, family = binomial())
exp(cbind(OR = coef(model_wm_only)))

                   OR
(Intercept) 0.2373923
geschlecht  2.2867514

Ziel: Die Auswirkung einer Erhöhung von $x_j$ um eine Einheit auf die Odds zu verstehen, ceteris paribus.
Der Logit (Log-Odds) für eine Beobachtung ist: \[ \ln(\text{Odds}) = \beta_0 + \dots + \beta_j x_j + \dots \]
Der Logit, wenn $x_j$ um 1 erhöht wird: \[ \ln(\text{Odds}_{\text{neu}}) = \beta_0 + \dots + \beta_j (x_j+1) + \dots \]
Die Differenz der Log-Odds ist exakt der Koeffizient: \[ \ln(\text{Odds}_{\text{neu}}) - \ln(\text{Odds}) = \beta_j \]
Das Verhältnis der Odds (Odds Ratio) ist somit: \[ \text{OR}_j = \frac{\text{Odds}_{\text{neu}}}{\text{Odds}} = e^{\beta_j} \]

Interpretation:

zeit: 1,1-fache höhere Chance zugunsten von Auto pro marg. höherer Zeit
geschlecht: 2,84-fache höhere Wskt./Chance dass ein Mann das Auto nimmt statt einer Frau
andere Variablen: nicht signifikant, aber Interpretation sonst wäre ähnlich
im Modell mit nur geschlecht: 2,287-fache höhere Wskt./Chance zugunsten von Mann siehe vorheriges Rechenbeispiel !

Modellgüte: Pseudo-$R^2$

Im Folgenden betrachten wir weitere Bestimmtheitsmaße, die ähnlich zu $R^2$ interpretiert werden können, die sogenannten Pseudo-$R^2$ Maße:

Cox & Snell ( R^2 ): Begrenzung auf ( [0, 0.75] )
Nagelkerke ( R^2 ): normiert, interpretiert wie klassisches ( R^2 ). Die Berechnung ist im R-Code unten dargestellt.

R-Umsetzung:

# Berechnung von Pseudo-R2;  install.packages("DescTools")
n <- length(model_1$residuals)
R2_cox_snell <- 1 - exp((model_1$deviance - model_1$null.deviance) / n)
R2_nagelkerke <- R2_cox_snell / (1 - exp(-(model_1$null.deviance / n)))
cbind(R2_cox_snell = R2_cox_snell, R2_nagelkerke = R2_nagelkerke)

     R2_cox_snell R2_nagelkerke
[1,]    0.3075782     0.4108907

DescTools::PseudoR2(model_1, which = "all")

       McFadden     McFaddenAdj        CoxSnell      Nagelkerke   AldrichNelson 
      0.2662381       0.2053693       0.3075782       0.4108907       0.2687707 
VeallZimmermann           Efron McKelveyZavoina            Tjur             AIC 
      0.4634518       0.3414064       0.4489603       0.3316623     130.5480618 
            BIC          logLik         logLik0              G2 
    144.4436793     -60.2740309     -82.1438532      43.7396445

Beispielwerte: $R^2_{\text{Cox-Snell}} = 0.308, R^2_{\text{Nagelkerke}} = 0.411$ $\hra$ Faustregel für $R^2_{\text{Nagelkerke}}$:
- < 0.2: Gering
- 0.2 - 0.4: Akzeptabel
- 0.4 - 0.5: Gut
- 0.5: Sehr gut

Modellgüte: Klassifizierungstabelle

Klassifizierungstabelle (Confusion Matrix)

Ein Schwellenwert (meist $\tau=0.5$) entscheidet über die Klassifikation: Falls die logistische Regression eine Wahrscheinlichkeit größer als 0.5 liefert, wird die Beobachtung als 1 klassifiziert, sonst als 0.

Figure 2: Klassifizierungstabelle / Wahrheitsmatrix / confusion matrix

\[ \begin{align*} \text{Sensitivität} &= \frac{\text{Richtig Positiv (TP)}}{\text{Richtig Positiv (TP)} + \text{Falsch Negativ (FN)}} = \frac{52}{52 + 17} = \frac{52}{69} \approx 0.7536232\\ \text{Spezifität} &= \frac{\text{Richtig Negativ (TN)}}{\text{Richtig Negativ (TN)} + \text{Falsch Positiv (FP)}} = \frac{38}{38 + 12} = \frac{38}{50} = 0.76 \end{align*} \]

Richtig Positive an Gesamt-Positiven: $52/64=81.25\%$
Richtig Negative an Gesamt-Negativen: $38/55=69.09\%$

Modellverbesserung und Modellvalidierung

Systematischer Ein- oder Ausschluss von Variablen

Nicht signifikante Variablen können aus dem Modell entfernt werden. Neben dem p-Wert aus der Modellzusammenfassung kann hierfür auch ein Wald-Test herangezogen werden.

# install.packages("survey")
survey::regTermTest(model_1, "umsteigen")

Wald test for umsteigen
 in glm(formula = mode ~ zeit + kosten + umsteigen + geschlecht, 
    family = binomial(), data = data_vkm)
F =  0.1583505  on  1  and  114  df: p= 0.69142

Sowohl der Regressionsoutput ($p=0.690680$) als auch das Wald-Testergebnis sollten in eine Gesamtevaluation einfließen.

Modellvalidierung

Wie gut sagt mein Modell tatsächlich die abhängige Variable voraus?
Cross-Validation: Man unterteilt den Datensatz k-fach in Test- und Trainingsdatensätze.
Das Modell wird mit dem Trainingsdatensatz geschätzt und die Vorhersage auf dem Testdatensatz evaluiert.
Dieser Prozess wird für verschiedene Modelle wiederholt und die Ergebnisse werden verglichen.

Idee und Einführung

Binär logistische Regression - Herleitungen

Modellgleichungen:

Odds (Oddsratio) und logarithmierte Odds (log-odds / logits):

Binär logistische Regression - Umsetzung in R

Nullmodell/Trainingsmodell vs. Testmodell

Interpretation

Nullmodellabweichung: Omnibus-Test

Modellgüte: Odds Ratio

Umsetzung in R:

Interpretation:

Modellgüte: Pseudo-\(R^2\)

Modellgüte: Klassifizierungstabelle

Klassifizierungstabelle (Confusion Matrix)

Modellverbesserung und Modellvalidierung

Systematischer Ein- oder Ausschluss von Variablen

Modellvalidierung

Binär logistische Regression - Umsetzung in `R`

Umsetzung in `R`: