Einige wichtige Grundbegriffe
Stationarität und Trend einer Zeitreihe
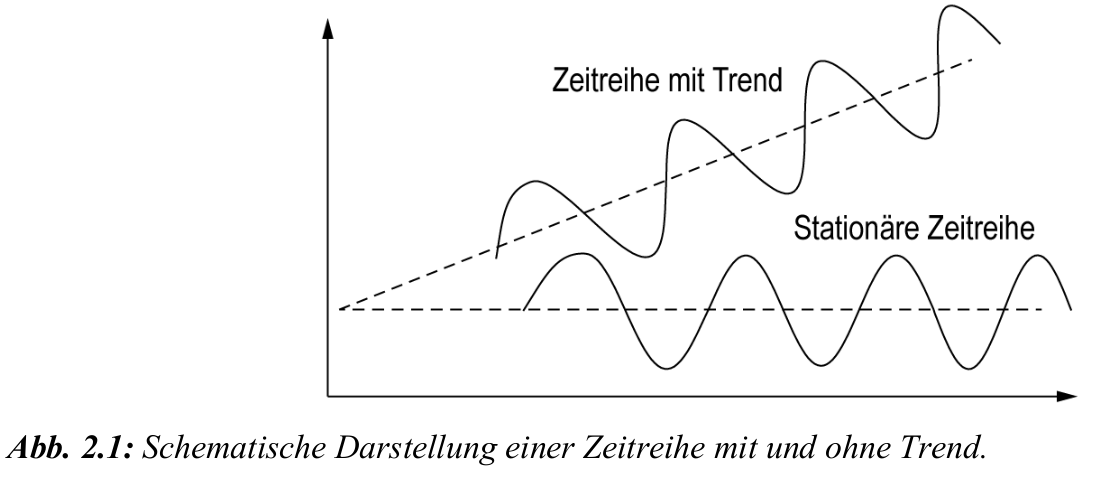
- Stationär: Mittelwert und Varianz bleiben über die Zeit konstant.
- Nicht-stationär: Zeitreihe zeigt Trend oder andere systematische Veränderungen.
- Stationäre Zeitreihen sind einfacher auszuwerten als nicht-stationäre.
- Nicht-stationäre Zeitreihen können durch Filtern oder Transformation stationär gemacht werden.
Saisonalität einer Zeitreihe
- Regelmäßige Schwankungen innerhalb bestimmter Zeiträume.
- Beispiel: Kursentwicklung an der Börse zeigt saisonale Effekte.
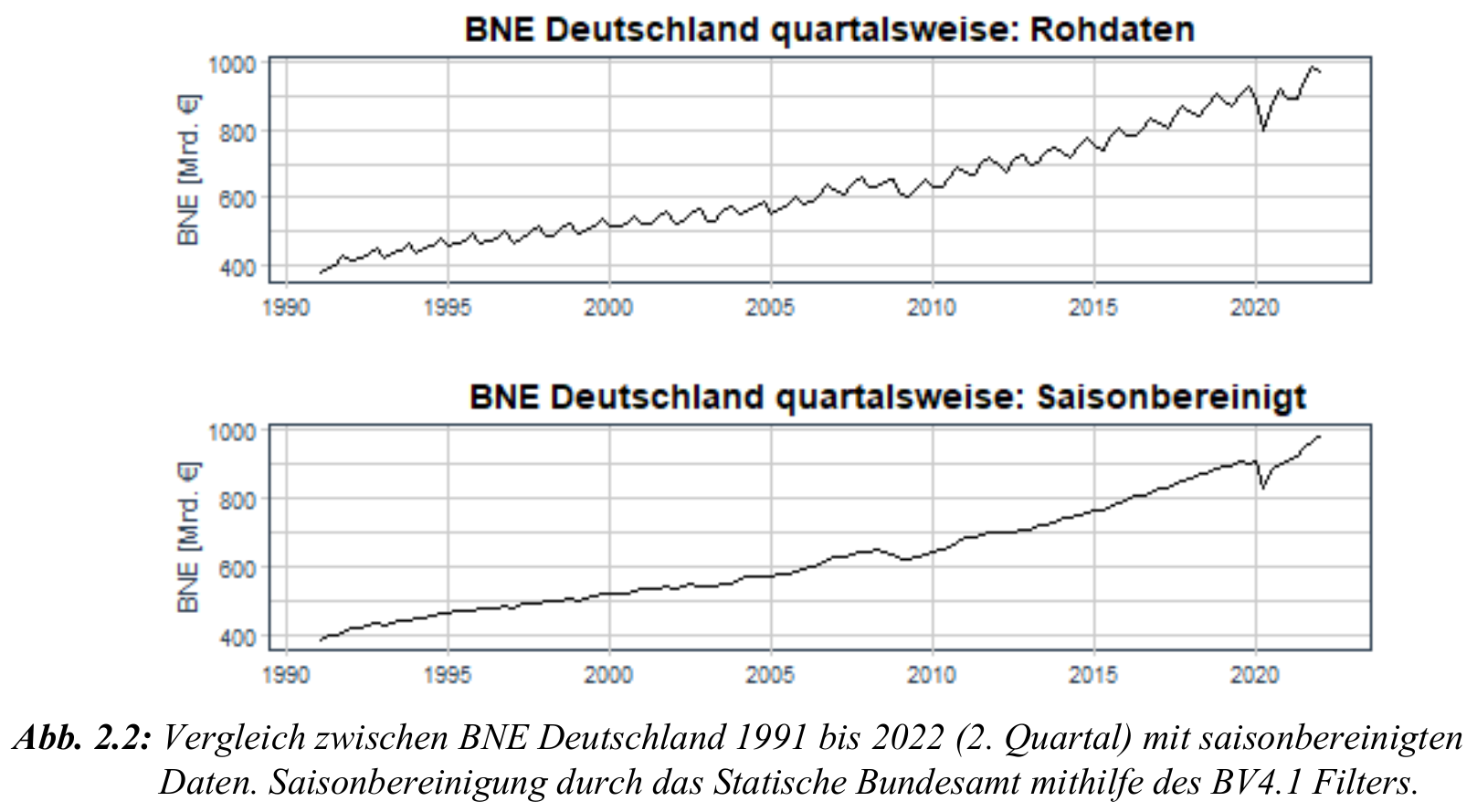
- Saisonalität kann Analyseergebnisse verfälschen, daher oft Saisonbereinigung notwendig.
- Statistisches Bundesamt nutzt BV4.1-Filter für Saisonbereinigung.
Autokorrelation, White Noise & Random Walk
Stochastische Grundbegriffe: Autokorrelation
Definition: Autokorrelation:
- Beschreibt den Zusammenhang zwischen Werten einer Zeitreihe und deren verzögerten Werten.
- Hohe Autokorrelation bedeutet, dass vergangene Werte stark mit aktuellen Werten zusammenhängen.
- Wichtig für Modellierung von Zeitreihen, da Abhängigkeiten über die Zeit hinweg berücksichtigt werden müssen.
Typischer Zeitreihenprozess: White Noise
Modell ohne Struktur oder Abhängigkeiten zwischen aufeinanderfolgenden Werten, d. h. Zufallsprozess mit konstantem Mittelwert und Varianz.
Mathematisch beschrieben als:
\[ x_t = M(t) + \epsilon_t, \quad \epsilon_t \overset{iid}{\sim} \mathbb{N}(0,\sigma^2) \]
Fehlerterm ( _t ) ist unabhängig und identisch verteilt (iid).
( M(t) ) beschreibt das Modell, z. B. additives Komponentenmodell: \(M(t) = x_T(t) + x_S(t) + x_R(t)\)
oder multiplikativ \(x_t = M(t) \cdot \epsilon_t\).Erweiterung durch Drift oder Trend möglich:
\[\begin{align*} x_t &= M(t) + \alpha + \epsilon_t \quad \text{Drift}\\ x_t &= M(t) + \beta \cdot t + \epsilon_t \quad \text{Trend}\\ x_t &= M(t) + \alpha + \beta \cdot t + \epsilon_t \quad \text{beides} \end{align*}\]
ACHTUNG:Unterstrichen Oft (siehe ARCH und GARCH Modelle am Ende des SB 03) wird \(M(t)\) weggelassen und ein starker WN angenommen:
\[\begin{align*} \mathbb{E}[x_t]&=0 \quad \text{und} \quad Var[x_t]=1 \\ \mathbb{E}[x_t x_s]&=0 \quad \text{bzw. } Cov[x_t,x_s]=0 \text{ für } t\neq s \\ x_t&\sim \mathcal{N}(0, 1) \end{align*}\]
Typischer Zeitreihenprozess: Random Walk
Modell, bei dem jeder Wert sich aus dem vorherigen Wert plus einer zufälligen Störgröße ergibt.
Mathematische Darstellung:
\[ x_t = x_{t-1} + \epsilon_t \]
Störgröße ( _t ) ist unabhängig und identisch verteilt (iid) mit:
\[ \mathbb{E}[\epsilon_t] = 0, \quad \text{Var}(\epsilon_t) = \sigma^2 \]
Erweiterung durch Drift:
\[ x_t = x_{t-1} + \alpha + \epsilon_t \]
Erweiterung durch Trend:
\[ x_t = x_{t-1} + \beta \cdot t + \epsilon_t \]
Kombination von Drift und Trend:
\[ x_t = x_{t-1} + \alpha + \beta \cdot t + \epsilon_t \]
Modell führt zu nicht-stationären Zeitreihen, da Varianz mit der Zeit wächst.
White Noise & Random Walk - Illustration
Vergleich Random Walk und White Noise
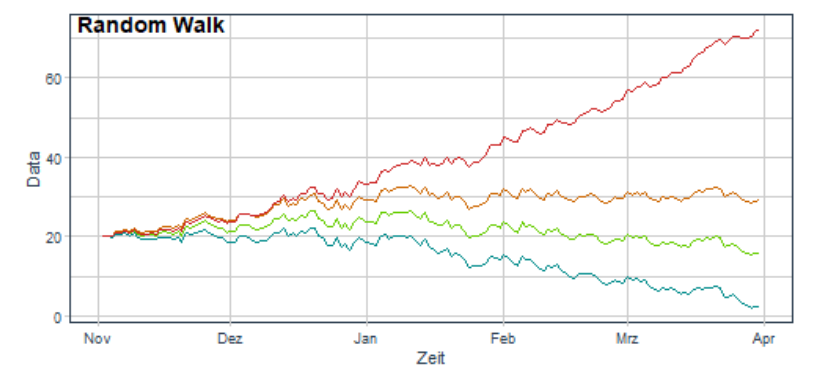
- Vier Random-Walk-Modelle erstellt:
- Basis: Startwert 20
- Modell mit positivem Drift ( +0,09 )
- Modell mit negativem Drift ( -0,09 )
- Modell mit zusätzlichem Trend ( 0,005 t )
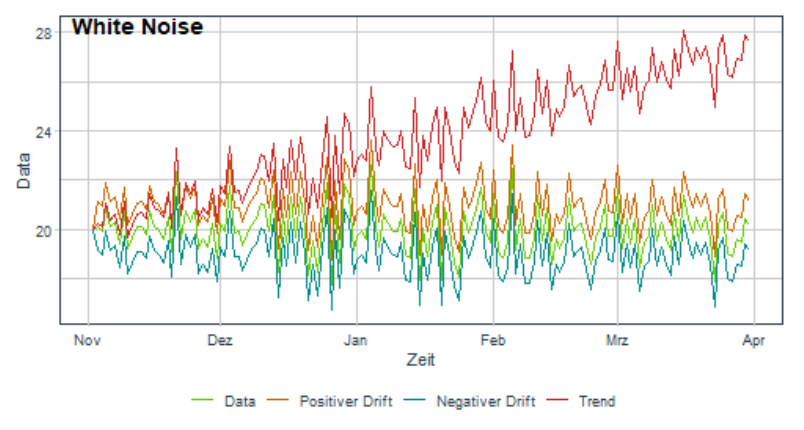
- Vier White-Noise-Modelle erstellt:
- Basis: Startwert 20
- Modell mit positivem Drift ( +1 )
- Modell mit negativem Drift ( -1 )
- Modell mit zusätzlichem Trend ( 0,005 t )
- Positiver Drift verschiebt die Werte nach oben, negativer Drift nach unten.
- Trend führt zu steigendem oder fallendem Verlauf der Zeitreihe.
- Unterschiede zwischen White Noise und Random Walk:
- Random Walk akkumuliert Störungen über die Zeit, Varianz wächst.
- White Noise bleibt um den Mittelwert stabil.
