Entscheidungsbäume: Grundidee

• Struktur zur Klassifikation oder Regression basierend auf Tests auf Attributwerten \(X_j\) \(\Rightarrow\) typische Anwendungen:

  • medizinische Diagnose
  • Kreditwürdigkeitsprüfung
  • Zielgruppenklassifikation im Marketing

• Ziel: herleitung einer regel, die Objekte korrekt einer Klasse \(K_m\) zuordnet

• jeder Pfad: Folge von Tests \(T_1, T_2, \dots\) auf Attribute; daraus entstehen Zweige, die zu einem Blatt führen

• formale Sicht: Entscheidungsbaum als Funktion zum Beispiel: \(f : \mathcal{X} \rightarrow \mathcal{Y}\) \[\begin{align*} f:~ \mathbb{R}^p &\rightarrow \{1, \dots, K\}\\ \bs{X} &\mapsto K_m \end{align*}\]

• Durch sukzessive Anwendung der Tests \(T_1, T_2,\ldots\) erhalten wir eine Aufteilung des Merkmalsraums \(\mathcal{X}\) in disjunkte Regionen \(R_1, \dots, R_M\) und somit am Ende \(f(\bs{X}) = K_m\) für potentielle komplett neue Objekte

• jedes Objekt wird eindeutig einem Blatt mit Klassenlabel zugeordnet

• Wurzelknoten: Startpunkt der Klassifikationsregel

• interner Knoten: Test auf Attributwert, z. B. \(X_2 < 0.53\)?

• Zweig: Ausprägung des Testergebnisses (z. B. „ja“ oder „nein“)

• Blattknoten: Ergebnis der Klassifikation

Beispiel: Entscheidungsbaum

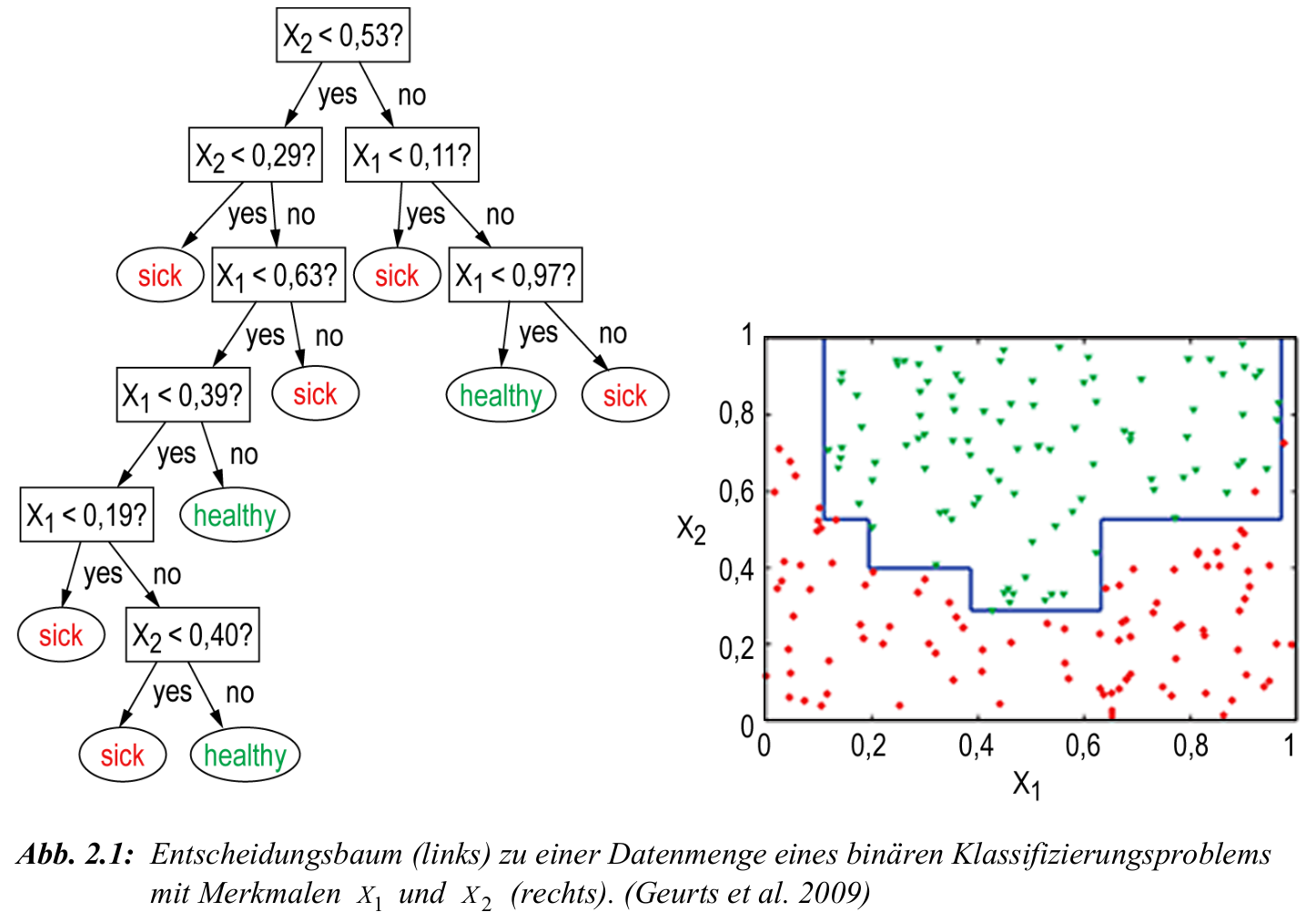
• rote Punkte: Klasse sick'' vs. grüne Punkte: Klassehealthy’’
• horizontale und vertikale Linien: durch Entscheidungsbaum induzierte Schwellenwerte
• Beispielpfad: \(X_2 < 0.53\) und \(X_1 < 0{,11}\) führt zur Klasse „sick“
• jeder Pfad im Baum definiert eine Region im Merkmalsraum
• Ziel: vollständige Trennung der Klassen durch einfache Tests auf Attributwerte

Induktionsaufgabe und Generalisierbarkeit

• Ziel: finde Klassifikationsregel \(f: \mathcal{X} \to \mathcal{Y}\), die neue Objekte korrekt einer Klasse zuordnet

• gegeben: Trainingsmenge \(M = \{(x_i, y_i)\}_{i=1}^N\) mit Attributen \(X_1, \dots, X_d\)

• gesucht: Entscheidungsbaum, der \(M\) korrekt trennt und auf ungesehene Daten generalisiert

• Voraussetzung: Attribute müssen Klassen unterscheidbar machen

• falls \(x_i = x_j\), aber \(y_i \neq y_j\): keine trennbare Klassifikation möglich

• Ziel ist nicht nur perfekte Trennung von \(M\), sondern robuste Generalisierung

• bei mehreren möglichen Bäumen wählt man den einfacheren

• Einfachheit gilt als Proxy für Generalisierungsfähigkeit

• Prinzip: Occam’s Razor – wähle die einfachste Hypothese, die zu den Daten passt

Aufspaltung eines Knotens

• sei \(M = \{(x_i, y_i)\}_{i=1}^N\) eine Trainingsmenge mit \(K\) Klassen

• sei \(A\) ein Attribut mit \(v\) Ausprägungen \(A_1, \dots, A_v\)

• aufteilung von \(M\) in Teilmengen \(M_1, \dots, M_v\) gemäß Attribut \(A\)

• \(M_j = \{ (x_i, y_i) \in M : x_i \text{ hat Attributwert } A_j \}\)

• für jeden Split-Knoten wird ein Attribut \(A\) gewählt, das \(M\) möglichst gut trennt also einen möglichst guten split erzeugt

• die Qualität eines Splits wird über Entropie und Informationsgewinn gemessen

• Ziel: maximale Homogenität der Klassen in den Teilmengen \(M_j\)

• Beispiel: wenn ein Attribut eine Partition erzeugt, in der jedes \(M_j\) nur eine Klasse enthält, ist der Informationsgewinn maximal

• falls alle Klassen gleich verteilt bleiben, ist der Split nutzlos

Entropie als Maß für Unreinheit

• Entropie misst die Unreinheit (Unsicherheit) einer Klassenzuordnung in \(M\)

• je gemischter die Klassenverteilung, desto höher die Entropie

• eine reine Menge (alle Objekte gleiche Klasse) hat Entropie \(= 0\)

• maximal bei Gleichverteilung: \(p_k = \frac{1}{K}\) für alle \(k = 1, \dots, K\)

• Entropie entspricht dem erwarteten Informationsgehalt einer zufälligen Klassenzuordnung

• Interpretation: wie „überraschend“ ist das Ergebnis einer Klassifikation?

• bei deterministischer Klasse (z. B. 100 % sick): keine Überraschung \(\rightarrow\) keine Information nötig

• bei Gleichverteilung (50/50): maximaler Überraschungseffekt \(\rightarrow\) mehr Information nötig

• Entropie liefert Grundlage für den Informationsgewinn eines Attributsplits

• je stärker ein Attribut die Entropie reduziert, desto besser ist es zur Trennung geeignet

Entropie und Informationsgewinn

• sei \(M\) eine Menge von Objekten, die auf \(K\) Klassen verteilt sind
• \(p_k\) sei der Anteil der Objekte (rel. Häufigkeit) in Klasse \(k\), \(k = 1, \dots, K\) und \(m_1,\ldots,m_K\) die entsprechende Anzahl der Objekte
• die Entropie von \(M\) ist definiert als: \[ H(M) = -\sum_{k=1}^{K} p_k \log_2 p_k \]
• \(H(M)\) misst die Unreinheit (Unsicherheit) der Klassenverteilung in \(M\)
• wie zuvor: \(A\) ist Attribut mit \(v\) Ausprägungen: \(a_1, \dots, a_v\) und \(M\) wird durch \(A\) in Teilmengen \(M_1, \dots, M_v\) aufgeteilt; dann ist die gewichtete Entropie nach Aufteilung durch \(A\): \[ H_A(M) = \sum_{j=1}^v \frac{|M_j|}{|M|} \cdot H(M_j)\quad\text{mit}\quad \frac{|M_j|}{|M|}=\frac{\sum_{k=1}^K m_{k}^{(j)}}{\sum_{k=1}^K m_k}\;, \]
• wobei \(m_{k}^{(j)}\) die Anzahl der Objekte aus Klasse \(k\) innerhalb \(M_j\) bezeichnet
• der Informationsgewinn durch Attribut \(A\) ist definiert als: \[ \text{gain}(A) = H(M) - H_A(M) \]
• \(A^* = \arg\max_{A \in \mathcal{A}} \, \text{gain}(A)\): bestes Attribut für Aufspaltung maximiert gain über Menge aller verfügbaren Attribute \(\mathcal{A}\)

Beispiel: Entropie und Informationsgewinn

• gegeben seien \(K=2\) Klassen: ‘’sick’’ und ‘’healthy’’ mit \(p_1\) als Anteil der Objekte in Klasse ‘’sick’’, \(p_2 = 1 - p_1\) für eine Menge von Objekten M

• Informationsgehalt eines Ereignisses \(z\) mit \(p(z)\) ist: \[ I_g(z) = -\log_2 p(z) \]

• Intuition: über ein wahrscheinliches Ereignis zu lernen ist weniger informativ als über ein unwahrscheinliches Ereignis zu lernen

• Entropie ist Erwartungswert des Informationsgehalts über alle Klassen und misst die Unbestimmtheit/Unreinheit der Klassenzugehörigkeit: \[ H(M) = p_1 \cdot I_g(p_1) + p_2 \cdot I_g(p_2) = -p_1 \log_2 p_1 - p_2 \log_2 p_2 \]

• Extremfall 1: \(p_1 = 1\), \(p_2 = 0\) \(\rightarrow\) \(H(M) = 0\) (vollständige Sicherheit)

• Extremfall 2: \(p_1 = p_2 = 0.5\) \(\rightarrow\) \(H(M) = 1\) (maximale Unsicherheit)

• Informationsgewinn durch ein Attribut \(A\): \[ \text{gain}(A) = H(M) - H_A(M) \]

• hoher Informationsgewinn von \(A\) erzeugt möglichst ‘’reinere’’ Teilmengen

• Ziel: maximale Reduktion der Unreinheit durch Auswahl des besten \(A^*\)

Beispiel: Fußball mit Entscheidungsbäumen

Day	Outlook	Temperature	Humidity	Wind	Play
D1	Sun	Hot	High	Low	No
D2	Sun	Hot	High	High	No
D3	Overcast	Hot	High	Low	Yes
D4	Rain	Sweet	High	Low	Yes
D5	Rain	Cool	Normal	Low	Yes
D6	Rain	Cool	Normal	High	No
D7	Overcast	Cool	Normal	High	Yes
D8	Sun	Sweet	High	Low	No
D9	Sun	Cool	Normal	Low	Yes
D10	Rain	Sweet	Normal	Low	Yes
D11	Sun	Sweet	Normal	High	Yes
D12	Overcast	Sweet	High	High	Yes
D13	Overcast	Hot	Normal	Low	Yes
D14	Rain	Sweet	High	High	No

Titel: Trainingsdaten für die Klassifikation: Wetterbedingungen und Spielergebnis

• Daten: Wetterbedingungen an 14 Tagen, d.h. \(M=14\) zu klassifizierende Objekte, mit Attributen:
  • Outlook: sun, overcast, rain
  • Temperature: hot, sweet, cool
  • Humidity: high, normal
  • Wind: high, low
• Zielvariable der Klassifikation: ‘’Play’’
  • \(\hookrightarrow\) Ausprägungen Yes es wurde Fußball gespielt vs. No, es wurde nicht gespielt

Beispiel: Fußball mit Entscheidungsbäumen

• Ziel: finde Attribut mit maximalem Informationsgewinn als Wurzelknoten
  • [1.] wir berechnen \(H(M)\)
  • [2.] anschließend \(H_{A_j}(M)\) für alle vier Attribute \(A_j\), \(j=1,\ldots,4\)
  • [3.] Attribut mit maximalem \(\text{gain}(A_j)\) bildet die Wurzel des Baums
  • [4.] splitte den Baum auf Basis der Attributwerte in Unterbäume
  • [5.] setze Schritte 2. - 4. fort, bis alle Elemente klassifiziert sind oder kein Informationsgewinn mehr möglich (Uneindeutigkeit des Klassifkationsproblems)

Klassenverteilung: 9 \(\times\) Yes, 5 \(\times\) No: \[\begin{align} H(M) &= -\frac{9}{14} \log_2 \frac{9}{14} - \frac{5}{14} \log_2 \frac{5}{14} \approx 0.940\\ H(M_{\text{sun}}) &= -\frac{2}{5} \log_2 \frac{2}{5} - \frac{3}{5} \log_2 \frac{3}{5} \approx 0.971 \\ H(M_{\text{overcast}}) & = -1 \cdot \log_2 1 = 0 \\ H(M_{\text{rain}}) &= -\frac{3}{5} \log_2 \frac{3}{5} - \frac{2}{5} \log_2 \frac{2}{5} \approx 0.971\\ \Rightarrow H_{\text{Outlook}}(M) &= \frac{5}{14} \cdot 0.971 + \frac{4}{14} \cdot 0 + \frac{5}{14} \cdot 0.971 \approx 0.693 \\ \Rightarrow \text{gain}(\text{Outlook}) &= H(M) - H_{\text{Outlook}}(M) = 0.940 - 0.693 = 0.247 \end{align}\]

Vergleich mit den anderen Informationsgewinnen:

gain(Temperature)=0.029, gain(Humidity)=0.152, gain(Wind)=0.048

Folge: Outlook wird als Wurzelknoten gewählt da gain(outlook)=0.247 am höchsten.

Beispiel: Fußball mit Entscheidungsbäumen

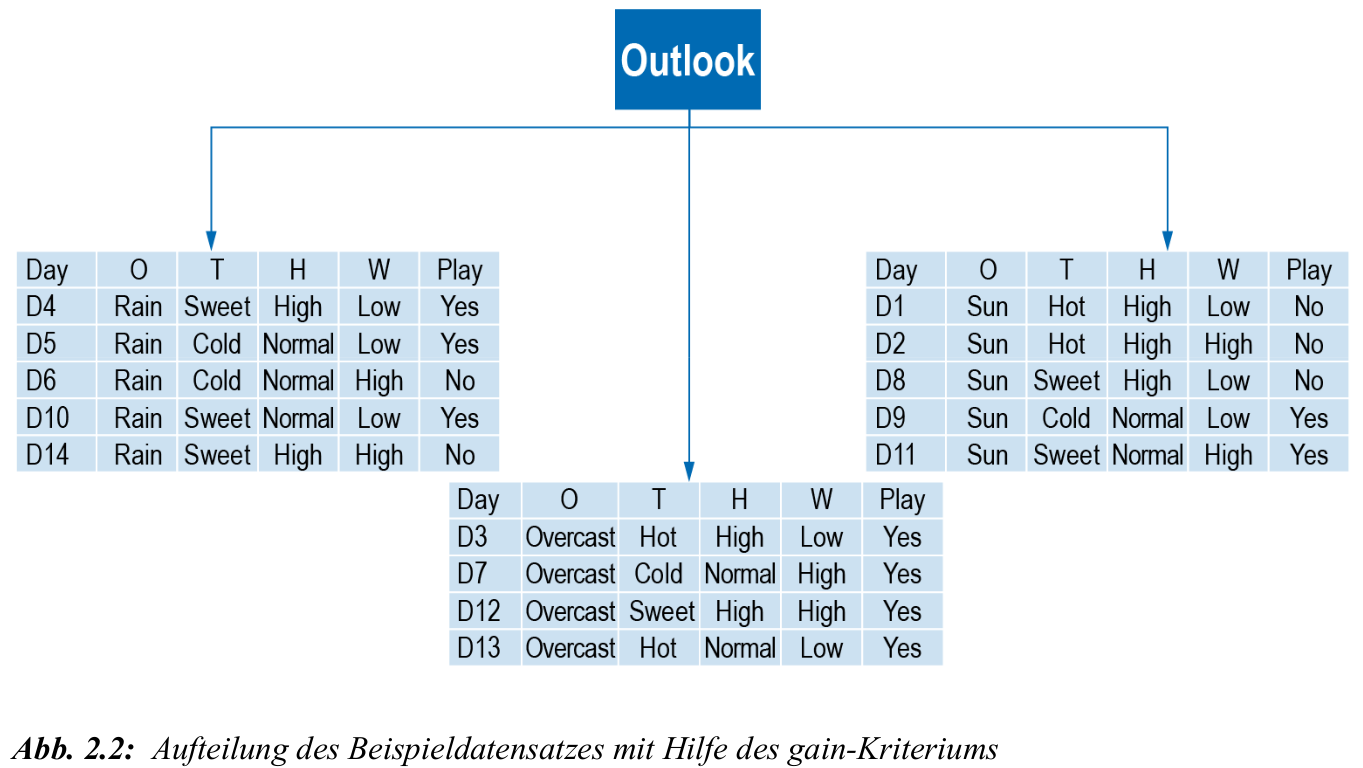
• nach dem ersten Attributsplit entstehen wieder Teilbäume (s. Abb. 2.2)
• für jeden dieser Teilbäume: erneut suchen des besten Attributs unter allen Attributen (einschließlich des ersten Outlook)
• Fortsetzung bis alle Objekte eindeutig klassifiziert sind oder kein Informationsgewinn mehr möglich ist, z.B. wenn weitere Klassifizierung nicht mehr möglich ist: danach zufällige Festsetzung oder Mehrheitsklasse

C4.5: Weiterentwicklung von ID3

• C4.5 verwendet wie ID3 Entropie als Kriterium, verbessert jedoch die Auswahl der Attribute

• Problem: Informationsgewinn bevorzugt Attribute mit vielen Ausprägungen

• Lösung: gainRatio als Quotient aus Informationsgewinn und Entropie der Aufteilung ‘’Split-Entropie’’: \[ \text{gainRatio}(A) = \frac{\text{gain}(A)}{\text{SplitEntropy}(A)} \]

• Split Entropy: misst die Informationsmenge zur Beschreibung der Aufteilung selbst: \[ \text{SplitEntropy}(A) = -\sum_{j=1}^v \frac{|M_j|}{|M|} \log_2 \frac{|M_j|}{|M|} \]

• je mehr mögliche Ausprägungen ein Attribut hat, desto höher die Split-Entropie

• Informationsgewinn allein belohnt ‘’überpräzise’’ Splits, z.B. durch ein Attribut mit fast eindeutigem Wert

• gainRatio normalisiert diesen Effekt und bevorzugt trennscharfe und gleichzeitig generalisierende Attribute

CART: Grundidee

• CART beginnt mit einem einzelnen Knoten \(L_0\) (der Wurzel) und Menge von Objekten \(M_0\) (\(=M\))
• jeder Knoten \(L_q\) verarbeitet eine Teilmenge \(M_q \subseteq M\) der Daten
• wenn alle Elemente in \(M_q\) die gleiche Klasse haben \(\rightarrow\) \(L_q\) wird Blatt
• falls für eine Untermenge \(M_q\) kein Informationsgewinn mehr möglich ist:
  • dann zufällige Festsetzung der Kategoriezugehörigkeit
  • oder Festsetzung der Kategoriezugehörigkeit mit Wert der Mehrheitskategorie
  • oder als Mittelwert über Kategorien (bei metrischen Werten z.B. Regressionsbäumen)
• sonst: wähle Attribut \(A_i\) unter allen Attributen, für \(i=1,\ldots,v\), mit Menge von Attributwerten \(\mathcal{A}_i\), sodass eine optimale Aufspaltung von \(M_q\) entsteht
  • \(\hookrightarrow\) Optimalitätsmaß: nicht Entropie sondern Gini-Index !
• es werden binäre Partitionen, d.h. Partitionen mit den Eigenschaften \(\mathcal{A}_i^L \cup \mathcal{A}_i^R = \mathcal{A}_i\), und \(\mathcal{A}_i^L \cap \mathcal{A}_i^R = \emptyset\) betrachtet; diese definieren dann auch eine Zerlegung von \(M_q\) zwei ebenfalls disjunkte Teilmengen: \[\begin{align} L_q^i(\mathcal{A}_i^L)&=\lbrace x^{(m)}\in M_q:a_i^{m}\in \mathcal{A}_i^L\rbrace\\ R_q^i(\mathcal{A}_i^R)&=\lbrace x^{(m)}\in M_q:a_i^{m}\in \mathcal{A}_i^R\rbrace \end{align}\]
• wobei \(a_i^{m}\) die konkrete Ausprägung eines Attributs \(A_i\) für ein zu klassifizierendes Input(-objekt) \(x^{(m)}\) bezeichnet und die Wahrscheinlichkeiten bzw. Anteile: \(p_{iL}^q(\mathcal{A}_i^L) = \frac{L_q^i(\mathcal{A}_i^L)}{M_q}\) und \(p_{iR}^q(\mathcal{A}_i^R) = 1 - p_{iL}^q(\mathcal{A}_i^L)\)

CART: Gini-Index und Knotenaufteilung

• Gini-Index misst Unreinheit in \(M_q\) mit Klassenanteilen \(p_k^q\): \[ Gini(M_q) = 1 - \sum_{k=1}^K (p_k^q)^2 \]

• minimale Unreinheit bei homogener Klassenzuordnung: \(Gini(M_q) = 0\)

• maximale Unreinheit bei Gleichverteilung: \(p_k^q = \frac{1}{K}\)

• Aufteilung von \(M_q\) in zwei Mengen über Zerlegung \(\mathcal{A}_i^L, \mathcal{A}_i^R\) und Berechnung eines gewichteten Gini-Index nach Aufteilung:

  \[\begin{align} wGini(M_q, \mathcal{A}_i^L) &= p_{iL}^q \cdot Gini(L_q^i(\mathcal{A}_i^L)) + p_{iR}^q \cdot Gini(R_q^i(\mathcal{A}_i^R))\\ Gini(L_q^i(\mathcal{A}_i^L)) &= 1 - \sum_{k=1}^K (p_{kL}^q(\mathcal{A}_i^L))^2\\ Gini(R_q^i(\mathcal{A}_i^R)) &= 1 - \sum_{k=1}^K (p_{kR}^q(\mathcal{A}_i^R))^2 \end{align}\]

CART: Gini-Gewinn und Optimierung

• Gini-Gewinn durch Partition \(\mathcal{A}_i^L \subset \mathcal{A}_i\): \[ GiniGain(M_q, \mathcal{A}_i^L) = Gini(M_q) - wGini(M_q, \mathcal{A}_i^L) \]
• Ziel: finde Partition mit maximalem Gini-Gewinn \[ \mathcal{A}_i^{L,*} = \arg\max_{\mathcal{A}_i^L \subset \mathcal{A}_i} \, GiniGain(M_q, \mathcal{A}_i^L) \]
• falls Gini-Gewinn = 0 \(\rightarrow\) keine sinnvolle Aufspaltung möglich und Knoten \(L_q\) erzeugt dann binäre Kinderknoten, basierend auf der gefundenen optimalen Partition induziert durch \(\mathcal{A}_i^{L,*}\)
• die binären Kinderknoten erhalten dann jeweils ihre zugehörigen Teilmengen \(M_L = L_q(\mathcal{A}_i^{L,*})\), \(M_R = R_q(\mathcal{A}_i^{L,*})\) und die Aufspaltung beginnt von neuem

CART: Eigenschaften und Pruning

• CART verwendet ausschließlich binäre Aufteilungen
• anwendbar auf numerische und kategoriale Attribute
  • bei numerischen Werten basiert Aufteilung auf einem threshold Wert der Form: \(x^{(m)} \leq t \quad \text{vs.} \quad x^{(m)} > t\)
  • kategoriale Merkmale werden in zwei Gruppen aufgeteilt z. B. \(\{\text{sun, rain}\}\) vs. \(\{\text{overcast}\}\)
    • dabei werden alle möglichen Kombinationen geprüft:
      • \(\{\text{sun, rain}\}\) vs. \(\{\text{overcast}\}\)
      • \(\{\text{sun}\}\) vs. \(\{\text{overcast, rain}\}\)
      • …
• erzeugte Bäume sind oft robuster als bei ID3
• zur Vermeidung von Overfitting wird Pruning eingesetzt:
  • Pre-Pruning: Stoppen der Aufspaltung bei geringer Stichprobengröße oder kleinem Gini-Gewinn
  • Post-Pruning: nachträgliches Zurückschneiden unnötiger Teilbäume
• Post-Pruning liefert in der Regel bessere Resultate

Regression mit Entscheidungsbäumen

• Ziel: Vorhersage einer numerischen Zielvariable, z. B. Anzahl Spieler

• Struktur des Baums wie bei CART: binäre Splits entlang von Attributen

• jeder Blattknoten enthält den arithmetischen Mittelwert der Zielvariable

• kein Klassenlabel, sondern reelle Vorhersagegröße

• Kriterium für Attributwahl: Varianzreduktion

• für Teilmenge \(M_q\): \[ \text{Var}(M_q) = \frac{1}{|M_q|} \sum_{i \in M_q} (y_i - \bar{y}_q)^2 \]

• Aufteilung in \(M_1\), \(M_2\) mit Gewichtung: \[ \text{Var}_{\text{split}} = \frac{|M_1|}{|M_q|} \text{Var}(M_1) + \frac{|M_2|}{|M_q|} \text{Var}(M_2) \]

• Ziel: maximale Reduktion der Varianz \[ \text{gain}_\text{Var} = \text{Var}(M_q) - \text{Var}_{\text{split}} \]

Beispiel: Fußball-Datensatz (Regression)

Day	Outlook	Temperature	Humidity	Wind	Players
D1	Sun	Hot	High	Low	25
D2	Sun	Hot	High	High	30
D3	Overcast	Hot	High	Low	46
D4	Rain	Sweet	High	Low	45
D5	Rain	Cool	Normal	Low	52
D6	Rain	Cool	Normal	High	23
D7	Overcast	Cool	Normal	High	43
D8	Sun	Sweet	High	Low	35
D9	Sun	Cool	Normal	Low	38
D10	Rain	Sweet	Normal	Low	46
D11	Sun	Sweet	Normal	High	48
D12	Overcast	Sweet	High	High	52
D13	Overcast	Hot	Normal	Low	44
D14	Rain	Sweet	High	High	30

Titel: Trainingsdaten für die Regression: Wetterbedingungen und Spieleranzahl

• Ziel: Vorhersage der Spieleranzahl (numerisch) \(\rightarrow\) Beispielattribut ‘’Outlook’’ mit drei Ausprägungen

Outlook	Anzahl	Mittelwert	Varianz	Std.-Abw.
Overcast	4	46.25	14.19	3.77
Rain	5	39.20	101.36	10.07
Sun	5	35.20	86.56	9.30

Titel: Spieleranzahl nach Outlook: Mittelwert, Varianz und Standardabweichung

Formel Varianz und Standardabweichung: \[ \text{Var}(M) = \frac{1}{n} \sum_{i=1}^n (y_i - \bar{y})^2\;,\quad \text{SD}(M) = \sqrt{\text{Var}(M)} \]

Beispiel: Fußball-Datensatz (Regression)

• Gesamtvarianz (korrekt): \(86.88\) Gesamt-Std.-Abw. (wie im SB): \(9.32\)
• gewichtete Varianz nach Outlook: \[\begin{align} \bar{y} &= \frac{1}{14} \sum_{i=1}^{14} y_i = \frac{607}{14} \approx 43.36 \\[1ex] \text{Var}(M) &= \frac{1}{14} \sum_{i=1}^{14} (y_i - \bar{y})^2 = \frac{1}{14} \left[ (25 - 43.36)^2 + (30 - 43.36)^2 + \dots + (30 - 43.36)^2 \right] \\ &= \frac{1}{14} \cdot 1216.26 \approx 86.88 \\[1ex] \text{SD}(M) &= \sqrt{86.88} \approx 9.32 \end{align}\]
• Varianzreduktion: \[ \text{gain}_\text{Var} = 86.88 - 67.31 = 19.57 \]
• gewichtete SD nach Outlook: \[ \text{SD}(M) = 9.32 \\[1ex] \text{SD}_{\text{split}} = \frac{5}{14} \cdot 9.30 + \frac{4}{14} \cdot 3.77 + \frac{5}{14} \cdot 10.07 = 3.32 + 1.08 + 3.26 = 7.66 \\[1ex] \]
• ‘’gain’’ auf Basis SD: \(\text{gain}_\text{SD} = 9.32 - 7.66 = 1.66\)
• Splitkriterium: Wähle Attribut mit maximaler Varianzreduktion, oder basierend auf Standardabweichung
• Blattwert: arithmetisches Mittel der Zielwerte in jedem Blatt

Random Forest

Ensemble von Entscheidungsbäumen

• Random Forest kombiniert viele Entscheidungsbäume zu einem Modell
• Idee: Bootstrapping + zufällige Attributauswahl pro Split
• jeder Baum wird auf einer Zufallsstichprobe der Daten trainiert
• bei jedem Split wird eine Zufallsauswahl von Attributen betrachtet
• Vorhersage bei Regression vs. Klassifikation: \[ \hat{y}_i = \frac{1}{T} \sum_{t=1}^T \hat{y}_{it}\;, \quad \hat{p}_i = \frac{1}{T} \sum_{t=1}^T I(\hat{y}_{it} = 1) \quad \Rightarrow \quad \hat{y}_i = \begin{cases} 1, & \hat{p}_i > 0.5 \\ 0, & \text{sonst} \end{cases}\;. \]

Random Forest: Eigenschaften

• reduziert die Varianz einzelner Bäume durch Aggregation
• robust gegenüber Rauschen und Overfitting
• keine Pruning-Strategien notwendig
• keine starke Parametrierung erforderlich (nur Anzahl Bäume \(T\) und Attributanzahl \(m\) pro Split)
• Ensemble-Vorhersagen sind oft genauer und stabiler als Einzelbäume
• Nachteile: geringe Interpretierbarkeit, hoher Rechenaufwand bei vielen Bäumen

Hyperparameter-Optimierung: Grundlagen

• Parameter: durch den Datensatz bestimmt, vom Algorithmus gelernt (z. B. Regressionskoeffizienten, Gewichte im neuronalen Netz)
• Hyperparameter: vom Anwender vor dem Training festgelegt, steuern das Lernverfahren
• Ziel der HPO: Wahl von Hyperparametern, die Modellgüte maximieren
• es gibt Verfahren ohne Hyperparameter (lineare Regression) und Verfahren ohne lernbare Parameter (k-nearest-neighbour), aber keine ohne beides
• typische HPO-Verfahren: grid search, random search, Bayessche Optimierung, gradientenbasierte Optimierung, evolutionäre Verfahren

Entscheidungsbaum: kurzer Überblick

• iterative Aufteilung des Datensatzes entlang Attributen bis zu Blättern
• Klassifikation: Datenpunkt folgt vom Wurzelknoten bis zum Blatt
• Problem: overfitting bei zu komplexen Bäumen

Zentrale Hyperparameter sind hier sog. Splittingkriterien

• criterion: gini, entropy, log_loss
• max_depth: maximale Tiefe des Baums zur Iomplexitätskontrolle
• min_samples_split: minimale Anzahl Datenpunkte für einen split

Datengrundlage für die Beispiele

• Datensatz: handgeschriebene Ziffern 0–9 (‘’Pen-Based Recognition of Handwritten Digits’’)
• 16 attribute als 4 \(\times\) 4-Pixel-Darstellung, werte 0–100
• Umfang: 10992 Beobachtungen, davon 7494 Trainings- und 3498 Test-Datenpunkte
• keine Fehlwerte (missing values)

Grid Search: Idee, Eigenschaften und Umsetzung für Entscheidungsbaum

• Prinzip: brute-force Prüfung aller Hyperparameter-kombinationen
• garantiertes Auffinden der besten Kombination im Raster
• Komplexität: viele parameter \(\times\) viele Ausprägungen \(\ra\) rasches Wachstum der Kombinationszahl
• Beispiel: 5 Hyperparameter \(\times\) 4 Werte \(\ra\) \(4^5 = 1\,024\) Kombinationen
• parallele Ausführung möglich, da Einzeltests unabhängig sind
• daten splitten: training und test
• suchraum
  • criterion \(\in \{\)gini, entropy, log_loss\(\}\)
  • max_depth \(\in \{1,\dots,10\}\)
  • min_samples_split \(\in \{2,\dots,10\}\)
• Schleifen über alle Kombinationen, Modell trainieren, accuracy auf Testdaten berechnen, beste Kombination merken
• optional Reproduzierbarkeit: random_state = 123

Grid Search: Beobachtung und Einsatzgrenzen

• Laufzeit steigt stark mit Suchraumgröße
• gut geeignet bei wenigen diskreten Hyperparametern
• Ergebnisse variieren leicht durch zufallseffekte in Datensplitting und Baumerzeugung
• beispielhafte Güte in der Anwendung: accuracy um ca. 88 % auf Testdaten